バンディットアルゴリズムで用いる集中不等式【マルコフ、チェビシェフ、ヘフディング】【信頼区間】

皆さんは、「たくさんのサイコロを振って出た目の平均を計算すると、だんだん期待値である3.5に近づいていく」という話を聞いたことがあるかもしれません。これは直感的に正しいように思えますよね。

この記事で学ぶ「測度の集中」とは、まさにこの直感を数学的に厳密に扱うための道具です。特に、機械学習や統計学では、手元にあるデータ（サンプルの集まり）から、まだ見ぬデータ全体（母集団）の性質を推測しようとします。例えば、ある薬の効果を調べるために100人に試した結果から、その薬が日本人全体にどれくらい効くのかを知りたい、といった状況です。

このとき、私たちが知りたいのは「100人の平均的な効果」が「日本人全体の本当の平均的な効果」から、どれくらいズレている可能性があるか、ということです。もし、偶然ものすごく薬が効く人ばかり100人集まってしまったら、私たちの推測は大きく外れてしまいますよね。

「測度の集中」に関する不等式（集中不等式）は、「データ（サンプル）の数が増えれば増えるほど、サンプルから計算した平均値が、本当の平均値から大きく外れる確率は、急激に小さくなる」ということを数学的に保証してくれます。

この文章では、その「確率」をどのように評価するのかを、簡単なものから強力なものへと順を追って見ていきます。

基本の確認 - 標本平均とそのばらつき

まずは、話の土台となる基本的な概念から確認しましょう。

確率変数と標本平均

ある試行（サイコロを振る、コインを投げるなど）の結果によって値が決まる変数を確率変数と呼びます。ここでは、$X$ という確率変数を考えます。例えば、$X$ はサイコロを1回振ったときの出目だと考えてみましょう。

この試行を $n$ 回独立に行った結果を $X_1, X_2, \dots, X_n$ とします。これらはすべて同じ確率の法則に従うと考えます（これを独立同分布 (i.i.d.) (independent and identically distributed)と言います）。

私たちは、この確率変数の「本当の平均値」、つまり期待値 $\mu = E[X]$ を知りたいとします。サイコロの例では、$\mu = (1+2+3+4+5+6)/6 = 3.5$ です。しかし、多くの場合、この $\mu$ は未知です。そこで、手元にある $n$ 個のデータを使って $\mu$ を推測します。その最も自然な方法が、データの平均を取ることです。これを標本平均（または経験平均）と呼び、$\hat{\mu}$ (ミュー・ハットと読みます) と書きます。

$$
\hat{\mu} = \frac{1}{n} \sum_{i=1}^{n} X_i = \frac{X_1 + X_2 + \dots + X_n}{n}
$$

標本平均の性質

この標本平均 $\hat{\mu}$ には、良い性質が2つあります。

１．不偏性 (Unbiasedness)

標本平均の期待値を取ると、なんと真の平均 $\mu$ に一致します。
$E[\hat{\mu}] = E\left[\frac{1}{n} \sum_{i=1}^{n} X_i\right] = \frac{1}{n} \sum_{i=1}^{n} E[X_i] = \frac{1}{n} \sum_{i=1}^{n} \mu = \frac{1}{n} (n\mu) = \mu$
これは、「平均的に見れば、標本平均は真の平均を正しく捉えている」ことを意味します。このような性質を持つ推定量を不偏推定量と呼びます。

２．分散の減少

標本平均がどれくらいばらつくか、つまり分散を計算してみましょう。確率変数 $X$ の分散を $\sigma^2 = V[X] = E[(X - \mu)^2]$ と書きます。$\sigma$ は標準偏差ですね。
標本平均の分散 $V[\hat{\mu}]$ は、各 $X_i$ が独立であることから、次のように計算できます。

$V[\hat{\mu}] = V\left[\frac{1}{n} \sum_{i=1}^{n} X_i\right] = \frac{1}{n^2} \sum_{i=1}^{n} V[X_i] = \frac{1}{n^2} \sum_{i=1}^{n} \sigma^2 = \frac{n\sigma^2}{n^2} = \frac{\sigma^2}{n}$

よって、次の重要な関係式が得られます。

$$
V[\hat{\mu}] = E[(\hat{\mu} - \mu)^2] = \frac{\sigma^2}{n} \quad (1)
$$

この式 (1) が教えてくれるのは、「データ数 $n$ を増やせば増やすほど、標本平均 $\hat{\mu}$ のばらつきは小さくなる」ということです。$n$ を4倍にすれば、ばらつき（分散）は1/4になります。これは、私たちの直感とも合致しますね。

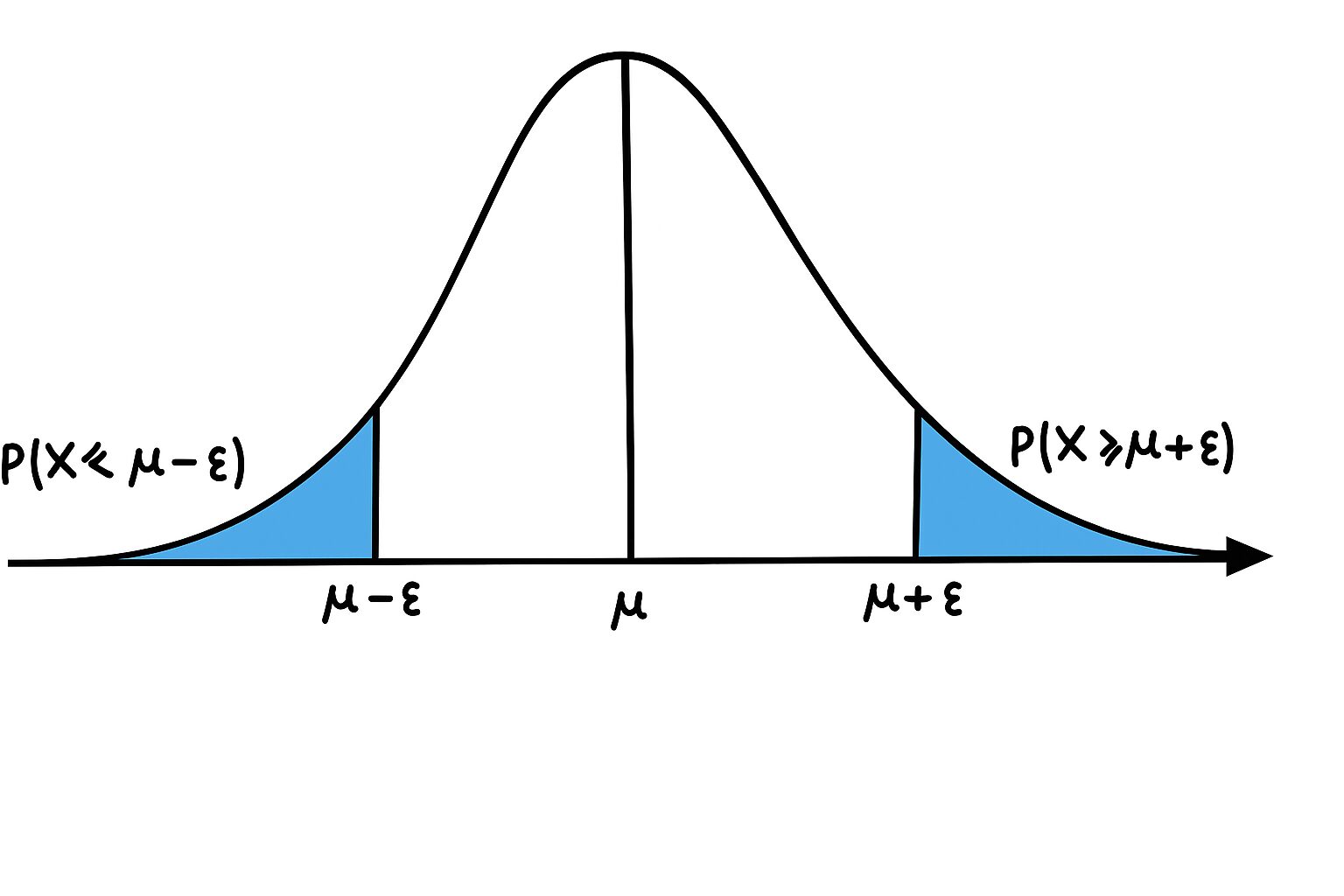
裾確率 (Tail Probabilities)

分散は「平均的なばらつき」を教えてくれますが、「標本平均 $\hat{\mu}$ が、真の平均 $\mu$ からものすごく大きく外れてしまう確率はどのくらいか？」ということまでは教えてくれません。この「大きく外れる確率」のことを裾確率 (Tail Probability) と呼びます。

具体的には、ある正の値 $\epsilon$ (イプシロンと読みます。小さな誤差を表すことが多いです) に対して、次のような確率を考えます。

$P(\hat{\mu} \ge \mu + \epsilon)$: 標本平均が、真の平均より $\epsilon$ 以上大きくなる確率（上側裾確率）
$P(\hat{\mu} \le \mu - \epsilon)$: 標本平均が、真の平均より $\epsilon$ 以上小さくなる確率（下側裾確率）
$P(|\hat{\mu} - \mu| \ge \epsilon)$: 標本平均と真の平均の差の絶対値が $\epsilon$ 以上になる確率（両側裾確率）

下の図は、確率分布の「裾」がどこを指すかを示したものです。平均 $\mu$ から離れた左右の端の部分が「裾」です。

これから、これらの裾確率を上から評価する（つまり、上限を求める）ための不等式を見ていきます。

マルコフとチェビシェフの不等式

裾確率を評価するための、最も基本的でどんな確率変数にも使える（その代わり、評価は少し甘い）ツールが、マルコフの不等式とチェビシェフの不等式です。

マルコフの不等式 (Markov's Inequality)

マルコフの不等式

任意の非負の確率変数 $Y$ と正の値 $\epsilon$ に対して、次の不等式が成り立ちます。

$$
P(Y \ge \epsilon) \le \frac{E[Y]}{\epsilon}
$$

絶対値を取ることで一般の確率変数 $X$ にも適用できます。
$$P(|X| \ge \epsilon) \le \frac{E[|X|]}{\epsilon}$$

これは、「平均値 $E[Y]$ が小さい確率変数が、非常に大きな値 $\epsilon$ を取る確率は、それに応じて小さくなる」という直感的な事実を数式にしたものです。

証明

非負の確率変数 $Y$ と $\epsilon>0$ をとる。指示関数 $I\{Y \geq \epsilon\}$ を用いると、いつでも

$$
Y \geq \epsilon I\{Y \geq \epsilon\}
$$

が成り立つ（事象 $\{Y \geq \epsilon\}$ では $Y \geq \epsilon$ 、補集合では左辺 $\geq 0$ 、右辺は 0 ）。両辺の期待値を取れば

$$
E[Y] \geq \epsilon P(Y \geq \epsilon)
$$

より

$$
P(Y \geq \epsilon) \leq \frac{E[Y]}{\epsilon}
$$

一般の確率変数 $X$ については $Y=|X|$ とすれぱ

$$
P(|X| \geq \epsilon) \leq \frac{E[|X|]}{\epsilon}
$$

を得る　□

チェビシェフの不等式 (Chebyshev's Inequality)

マルコフの不等式は非常に強力で、これを少し工夫することで、分散を使ったもっと便利な不等式を導くことができます。それがチェビシェフの不等式です。

チェビシェフの不等式

確率変数 $X$ の期待値を $\mu$、分散を $\sigma^2$ とします。このとき、任意の正の値 $\epsilon$ に対して、

$$
P(|X - \mu| \ge \epsilon) \le \frac{\sigma^2}{\epsilon^2}
$$

$$P(|X - E[X]| \ge \epsilon) \le \frac{V[X]}{\epsilon^2}$$

が成り立ちます。これは、「分散（ばらつき）が小さい確率変数は、その平均値から大きく外れる確率も小さい」という、これまた直感的な事実を表しています。

証明

$\mu=E[X]$ とし、非負確率変数 $Y^2=(X-\mu)^2$ にマルコフの不等式を適用する：

$$
P(Y^2 \ge \epsilon^2) \le \frac{E[Y^2]}{\epsilon^2}
$$

$$
P\left((X-\mu)^2 \geq \epsilon^2\right) \leq \frac{E\left[(X-\mu)^2\right]}{\epsilon^2}=\frac{V[X]}{\epsilon^2} .
$$

左辺は $P(|X-\mu| \geq \epsilon)$ に等しいので

$$
P(|X-\mu| \geq \epsilon) \leq \frac{V[X]}{\epsilon^2}
$$

□

このチェビシェフの不等式を、私たちの興味の対象である標本平均 $\hat{\mu}$ に適用してみましょう。$\hat{\mu}$ の期待値は $\mu$、分散は $V[\hat{\mu}] = \sigma^2/n$ でしたから、これらを代入すると、

$$
P(|\hat{\mu} - \mu| \ge \epsilon) \le \frac{V[\hat{\mu}]}{\epsilon^2} = \frac{\sigma^2}{n\epsilon^2} \quad (2)
$$

この式 (2) は、標本平均 $\hat{\mu}$ が真の平均 $\mu$ から $\epsilon$ 以上離れる確率の上限を与えてくれます。
注目すべきは、右辺が $1/n$ に比例している点です。つまり、データ数 $n$ を2倍にすれば、誤差が $\epsilon$ 以上になる確率の上限は半分になります。これは、データが増えるほど推定が正確になることを保証する、最初の重要な結果です。

しかし、このチェビシェフの不等式は、どんな分布にも使える万能なものである代わりに、評価が甘い（上限が大きすぎる）という弱点があります。もっとシャープな評価はできないでしょうか？

中心極限定理

チェビシェフの不等式よりも強力な評価を与えるヒントが、確率論の王様とも言える中心極限定理 (Central Limit Theorem, CLT) です。

中心極限定理 (CLT)

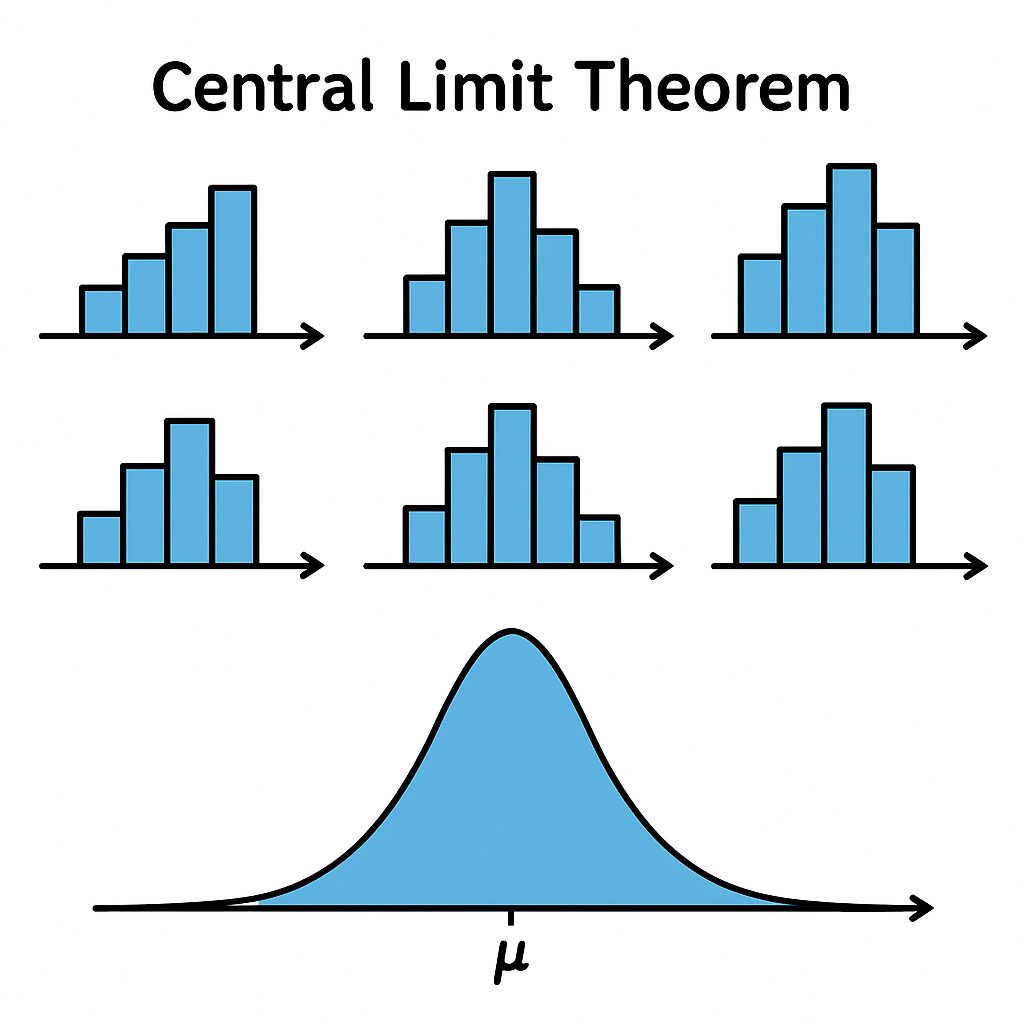
中心極限定理をざっくり言うと、「元の確率変数がどんな分布に従っていても、その独立なコピーをたくさん足し合わせたもの（あるいはその平均）は、正規分布（ガウス分布）に近づく」という驚くべき定理です。

数式で書くと、$S_n = \sum_{i=1}^n (X_i - \mu)$ という量を考えたとき、$n$ が非常に大きくなると、$S_n / \sqrt{n\sigma^2}$ という確率変数の分布が、平均0、分散1の標準正規分布 $N(0, 1)$ に従う、ということです。

正規分布の裾確率は、指数関数的に非常に速くゼロに近づくことが知られています。平均0、分散1の正規分布に従う確率変数 $Z$ の裾確率は、次のように評価できます。

$$
P(Z \ge u) = \int_u^\infty \frac{1}{\sqrt{2\pi}} \exp\left(-\frac{x^2}{2}\right) dx \le \frac{1}{u\sqrt{2\pi}} \exp\left(-\frac{u^2}{2}\right) \quad (3)
$$

この計算について

ポイントは $u>0$ のとき，正規分布の確率密度 $\phi(x)=\frac{1}{\sqrt{2 \pi}} e^{-x^2 / 2}$ の＂微分＂が $\phi^{\prime}(x)=-x \phi(x)$ になることと，区間 $[u, \infty)$ では $1 / x \leq 1 / u$ が成り立つことを使うことです

$x \geq u>0$ なら $1 / x \leq 1 / u$ なので，

$$
P(Z \geq u)=\int_u^{\infty} \phi(x) d x=\int_u^{\infty} \frac{1}{x} x \phi(x) d x \leq \frac{1}{u} \int_u^{\infty} x \phi(x) d x
$$

ところが

$$
\int_u^{\infty} x \phi(x) d x=\frac{1}{\sqrt{2 \pi}} \int_u^{\infty} x e^{-x^2 / 2} d x=\frac{1}{\sqrt{2 \pi}}\left[-e^{-x^2 / 2}\right]_{x=u}^{\infty}=\frac{1}{\sqrt{2 \pi}} e^{-u^2 / 2}
$$

したがって

$$
P(Z \geq u) \leq \frac{1}{u} \cdot \frac{1}{\sqrt{2 \pi}} e^{-u^2 / 2}=\frac{1}{u \sqrt{2 \pi}} e^{-u^2 / 2} .
$$

これが（3）です。□

この不等式は、右辺に $\exp(-u^2/2)$ という項があるため、uが大きくなると確率がものすごい勢いで小さくなることを示しています。

中心極限定理を使った裾確率の評価

この中心極限定理を使って、標本平均の裾確率を評価してみましょう。

$P(\hat{\mu} \ge \mu + \epsilon) = P(\frac{1}{n}\sum X_i \ge \mu + \epsilon) = P(\sum (X_i - \mu) \ge n\epsilon) = P\left(\frac{\sum (X_i - \mu)}{\sqrt{n\sigma^2}} \ge \frac{n\epsilon}{\sqrt{n\sigma^2}}\right)$

中心極限定理によれば、左辺の確率変数は $Z \sim N(0,1)$ に近似できるので、

$P(\hat{\mu} \ge \mu + \epsilon) \approx P\left(Z \ge \frac{\epsilon\sqrt{n}}{\sigma}\right)$

となります。ここに式 (3) を適用すると ($u = \epsilon\sqrt{n}/\sigma$ として)、

$$
P(\hat{\mu} \ge \mu + \epsilon) \le \sqrt{\frac{\sigma^2}{2\pi n \epsilon^2}} \exp\left(-\frac{n\epsilon^2}{2\sigma^2}\right) \quad (4)
$$

この評価式 (4) を見てください！右辺には $\exp(-n\epsilon^2/(2\sigma^2))$ という項があります。これは、データ数 $n$ が増えると、裾確率が指数関数的に減少することを示唆しています。これは、チェビシェフの不等式の $1/n$ での減少よりもはるかに速い、非常に強力な結果です。

中心極限定理の落とし穴

しかし、中心極限定理にも弱点があります。中心極限定理はあくまで $n$ が無限大に近づくときの極限の話です。私たちが実際に使うデータ数 $n$ は有限です。$n$ が小さいときや、元の分布の形が特殊な場合には、正規分布による近似は全く当てにならないことがあります。

したがって、アルゴリズムの性能を厳密に保証したい場合には、「$n$ がどんな値でも成り立つ」不等式が必要です。そこで登場するのが、次の章で学ぶ「劣ガウス性」という考え方です。

劣ガウス性とヘフディングの不等式

中心極限定理は「どんな分布でも、たくさん足せば正規分布っぽくなる」というものでしたが、発想を転換して、「もし元の確率変数が、そもそも正規分布に似た性質を持っていたらどうだろう？」と考えてみましょう。この「正規分布に似た性質」を数学的に定式化したのが劣ガウス性 (Subgaussianity) です。

劣ガウス性の定義

確率変数 $X$ のモーメント生成関数 $M_X(\lambda) = E[\exp(\lambda X)]$ を考えます。（$\lambda$ はラムダと読む実数のパラメータです）。これは、確率変数を指数関数に入れてから期待値を取ったもので、分布の様々な性質を調べるのに役立ちます。

【定義】劣ガウス性

ある確率変数 $X$ (ここでは簡単のため $E[X]=0$ とします) が $\sigma$-劣ガウス ($\sigma$-subgaussian) であるとは、すべての実数 $\lambda$ に対して、次の不等式が成り立つことを言います。

$$
E[\exp(\lambda X)] \le \exp\left(\frac{\lambda^2 \sigma^2}{2}\right)
$$

この式の右辺は、平均0、分散$\sigma^2$の正規分布のモーメント生成関数と全く同じ形です。つまり、劣ガウス性とは、「その確率変数のモーメント生成関数が、同じ分散を持つ正規分布のモーメント生成関数で上から抑えられる」という性質なのです。これにより、裾が正規分布と同じか、それ以上に軽く（急速にゼロに近づく）ことが保証されます。

劣ガウスの性質

1．スケーリング：任意の定数 $c \in \mathbb{R}$ に対して、 $c X$ は $|c| \sigma$－劣ガウス。
2．独立和：独立な $X_1, X_2$ がそれぞれ $\sigma_1, \sigma_2$－劣ガウスなら、 $X_1+X_2$ は $\sqrt{\sigma_1^2+\sigma_2^2}$－劣ガウス。
3．（一般の）独立線形結合：独立な $X_i$ が $\sigma_i$－劣ガウス、係数 $a_i \in \mathbb{R}$ とすると、

$$
\sum_{i=1}^n a_i X_i \text { は }\left(\sqrt{\sum_{i=1}^n a_i^2 \sigma_i^2}\right) \text {-劣ガウス. }
$$

特に、すべて $\sigma$－劣ガウスなら $\sum a_i X_i$ は $\sigma \sqrt{\sum a_i^2}$－劣ガウス。

証明

1．$E\left[e^{\lambda(c X)}\right]=E\left[e^{(c \lambda) X}\right] \leq \exp \left((c \lambda)^2 \sigma^2 / 2\right)$ より直ちに従う。
2．独立性から $E\left[e^{\lambda\left(X_1+X_2\right)}\right]=E\left[e^{\lambda X_1}\right] E\left[e^{\lambda X_2}\right] \leq \exp \left(\lambda^2\left(\sigma_1^2+\sigma_2^2\right) / 2\right)$ 。
3．同様に独立性と 1．を繰り返し用いれぱ

$$
E\left[\exp \left(\lambda \sum_{i=1}^n a_i X_i\right)\right]=\prod_{i=1}^n E\left[e^{\lambda a_i X_i}\right] \leq \prod_{i=1}^n \exp \left(\frac{\lambda^2 a_i^2 \sigma_i^2}{2}\right)=\exp \left(\frac{\lambda^2}{2} \sum_{i=1}^n a_i^2 \sigma_i^2\right) .
$$

劣ガウスな確率変数の例

どんな確率変数が劣ガウスなのでしょうか？

正規分布 (ガウス分布): 平均0、分散$\sigma^2$の正規分布は、定義そのものから$\sigma$-劣ガウスです。
有界な確率変数: これが非常に重要です。もし確率変数 $X$ の取る値が必ず区間 $[a, b]$ の中に収まるなら（例えば、コイントスなら{0, 1}、ルーレットなら{0, ..., 36}）、その確率変数は劣ガウスになります。具体的には、$(b-a)/2$-劣ガウスであることが示せます（ヘフディングの補題 (Hoeffding's Lemma)）。

ヘフディングの補題の証明

まず $e^{\lambda x}$ は下に凸なので、任意の $x \in[a, b]$ で

$$
e^{\lambda x} \leq \frac{b-x}{b-a} e^{\lambda a}+\frac{x-a}{b-a} e^{\lambda b}
$$

両辺の期待値をとり、 $\mu=E[X], \gamma=(\mu-a) /(b-a) \in[0,1]$ とおくと

$$
E\left[e^{\lambda X}\right] \leq(1-\gamma) e^{\lambda a}+\gamma e^{\lambda b}
$$

これを中心化して

$$
E\left[e^{\lambda(X-\mu)}\right]=e^{-\lambda \mu} E\left[e^{\lambda X}\right] \leq \exp \left(-\lambda \mu+\log \left((1-\gamma)+\gamma e^{\lambda(b-a)}\right)\right) .
$$

ここで

$$
L(t):=-\gamma t+\log \left((1-\gamma)+\gamma e^t\right), \quad t=\lambda(b-a),\quad \gamma \in[0,1] $$

とおくと、

$$
\begin{aligned}
L(0)=0, & L^{\prime}(t)=-\gamma+\frac{\gamma e^t}{(1-\gamma)+\gamma e^t}, \quad L^{\prime}(0)=0 \\
L^{\prime \prime}(t) & =\frac{\gamma(1-\gamma) e^t}{\left((1-\gamma)+\gamma e^t\right)^2}>0
\end{aligned}
$$

が成り立ち、Lは下に凸で、さらに

$$
L^{\prime \prime}(t)=\frac{\gamma(1-\gamma) e^t}{\left((1-\gamma)+\gamma e^t\right)^2} \leq \frac{1}{4}
$$

$(\gamma(1-\gamma) \leq 1 / 4$ を用いた）が言える。これで

$$
L(t) \leq \frac{t^2}{2} \sup _{s \in[0, t]} L^{\prime \prime}(s) \leq \frac{t^2}{8} \qquad \text{※}
$$

以上より

$$
E\left[e^{\lambda(X-\mu)}\right] \leq \exp \left(\frac{\lambda^2(b-a)^2}{8}\right)
$$

□

※

$L$ は $C^2$ で $L(0)=L^{\prime}(0)=0$ なので、積分の基本定理を 2 回使うと

$$
L^{\prime}(t)=\int_0^t L^{\prime \prime}(s) d s, \quad L(t)=\int_0^t L^{\prime}(u) d u=\int_0^t \int_0^u L^{\prime \prime}(s) d s d u=\int_0^t(t-s) L^{\prime \prime}(s) d s
$$

が得られます（「二次のテイラー展開の積分形」：$L(t)=\frac{1}{2} L^{\prime \prime}(\xi) t^2$ と書いても良い）。
ここで、 $t \geq 0$ とすると

$$
0 \leq(t-s) \leq t \quad(s \in[0, t])
$$

より

$$
L(t)=\int_0^t(t-s) L^{\prime \prime}(s) d s \leq\left(\sup _{s \in[0, t]} L^{\prime \prime}(s)\right) \int_0^t(t-s) d s=\frac{t^2}{2} \sup _{s \in[0, t]} L^{\prime \prime}(s)
$$

$\left(t<0\right.$ の場合も同様に $\int_t^0(0-s) L^{\prime \prime}(s) d s$ と書けば、区間を $[t, 0]$ に変えるだけで同じ結論になります。）

Cramér-Chernoff法と裾確率の評価

劣ガウス性という強力な仮定のもとで、裾確率を評価する必殺技が Cramér-Chernoff法です。これは次のようなステップで行われます。

【定理Cramer-Chernoff】

$X$ が平均0の $\sigma$-劣ガウス確率変数であるとき、任意の $\epsilon \ge 0$ に対して、

$$
P(X \ge \epsilon) \le \exp\left(-\frac{\epsilon^2}{2\sigma^2}\right) \quad (5)
$$

が成り立ちます。

証明

任意の $\lambda>0$ について

$$
P(X \geq \epsilon)=P\left(e^{\lambda X} \geq e^{\lambda \epsilon}\right) \leq \frac{E\left[e^{\lambda X}\right]}{e^{\lambda \epsilon}} \quad \text { (マルコフの不等式). }
$$

$X$ は $\sigma$－劣ガウスなので $E\left[e^{\lambda X}\right] \leq \exp \left(\lambda^2 \sigma^2 / 2\right)$ 。したがって

$$
P(X \geq \epsilon) \leq \exp \left(\frac{\lambda^2 \sigma^2}{2}-\lambda \epsilon\right) \quad(\forall \lambda>0)
$$

右辺を $\lambda$ で最小化する（凸二次関数）。導関数を0におけば $\lambda^{\star}=\epsilon / \sigma^2$ で、これを代入して

$$
P(X \geq \epsilon) \leq \exp \left(-\frac{\epsilon^2}{2 \sigma^2}\right)
$$

同様に $P(X \leq-\epsilon) \leq \exp \left(-\epsilon^2 /\left(2 \sigma^2\right)\right)$ 。したがって

$$
P(|X| \geq \epsilon) \leq 2 \exp \left(-\frac{\epsilon^2}{2 \sigma^2}\right)
$$

も従う□

この結果 (5) は、中心極限定理が示唆していた指数的な減衰を、有限のサンプル数で、しかも近似なしに保証する、非常に強力なものです。

標本平均への応用 (ヘフディングの不等式)

この素晴らしい結果を標本平均 $\hat{\mu}$ に応用しましょう。
そのためには、劣ガウス確率変数の和がどうなるかを知る必要があります。

【補題】劣ガウスの標本平均

独立な確率変数 $X_1, \dots, X_n$ がすべて平均0の $\sigma$-劣ガウスであるとします。このとき、その和を $n$ で割った $\frac{1}{n}\sum_{i=1}^n X_i$ は、$\frac{\sigma}{\sqrt{n}}$-劣ガウスになります。

証明

独立な平均 0 の $\sigma$－劣ガウス $X_1, \ldots, X_n$ を考える。独立性より

$$
E\left[\exp \left(\lambda \cdot \frac{1}{n} \sum_{i=1}^n X_i\right)\right]=\prod_{i=1}^n E\left[e^{(\lambda / n) X_i}\right] \leq \prod_{i=1}^n \exp \left(\frac{(\lambda / n)^2 \sigma^2}{2}\right)=\exp \left(\frac{\lambda^2(\sigma / \sqrt{n})^2}{2}\right)
$$

ゆえに $\frac{1}{n} \sum_{i=1}^n X_i$ は $\sigma / \sqrt{n}$－劣ガウス。平均が $\mu$ の場合は各 $X_i-\mu$ に適用すればよい。□

この補題は、標本平均の誤差 $\hat{\mu} - \mu = \frac{1}{n} \sum_{i=1}^n (X_i - \mu)$ が、$\frac{\sigma}{\sqrt{n}}$-劣ガウスであることを意味します（各 $X_i - \mu$ は平均0の $\sigma$-劣ガウスと仮定）。

したがって、【定理Cramer-Chernoff】の $X$ を $\hat{\mu} - \mu$ に、$\sigma$ を $\sigma/\sqrt{n}$ に置き換えることで、次の結論が得られます。

【系】ヘフディングの不等式

$X_i - \mu$ が独立な $\sigma$-劣ガウス確率変数であると仮定します。このとき、任意の $\epsilon \ge 0$ に対して、

$$
P(\hat{\mu} \ge \mu + \epsilon) \le \exp\left(-\frac{n\epsilon^2}{2\sigma^2}\right)
$$
$$
P(\hat{\mu} \le \mu - \epsilon) \le \exp\left(-\frac{n\epsilon^2}{2\sigma^2}\right)
$$

が成り立ちます。

これはヘフディングの不等式 (Hoeffding's inequality) の一種であり、ここで紹介される集中不等式の中でも特に重要で、広く使われているものです。

信頼区間という考え方

ヘフディングの不等式は、別の見方をすることもできます。
$P(\hat{\mu} \ge \mu + \epsilon) \le \delta$ という形にしたいとき、$\delta = \exp(-\frac{n\epsilon^2}{2\sigma^2})$ とおけば良いことがわかります。この式を $\epsilon$ について解くと、$\epsilon = \sqrt{\frac{2\sigma^2 \log(1/\delta)}{n}}$ となります。

これを言い換えると、

「確率 $1-\delta$ 以上で、$\hat{\mu} \le \mu + \sqrt{\frac{2\sigma^2 \log(1/\delta)}{n}}$ が成り立つ」
これは、真の平均 $\mu$ の上側信頼区間を与える式と見なせます。

$$
\mu \le \hat{\mu} + \sqrt{\frac{2\sigma^2 \log(1/\delta)}{n}} \quad (6)
$$

同様に、下側裾確率から、

$$
\mu \ge \hat{\mu} - \sqrt{\frac{2\sigma^2 \log(1/\delta)}{n}} \quad (7)
$$

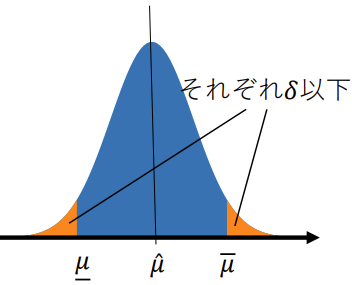
が得られます。これらは、「高い確率（$1-\delta$）で、真の平均 $\mu$ は、観測された標本平均 $\hat{\mu}$ を中心とするこの範囲内に収まっている」ということを主張しており、統計的な推測の基礎となる非常に重要な式です。

まとめ

「測度の集中」は、一見すると抽象的で難しい数式が並んでいるように見えるかもしれません。しかし、その根底にあるのは「たくさんのサンプルを集めれば、その平均は本当の平均に強く『集中』する」というシンプルで力強いアイデアです。このアイデアを数学的に表現したものが集中不等式であり、不確実なデータから確かな結論を導き出すための、現代科学に不可欠なツールなのです。