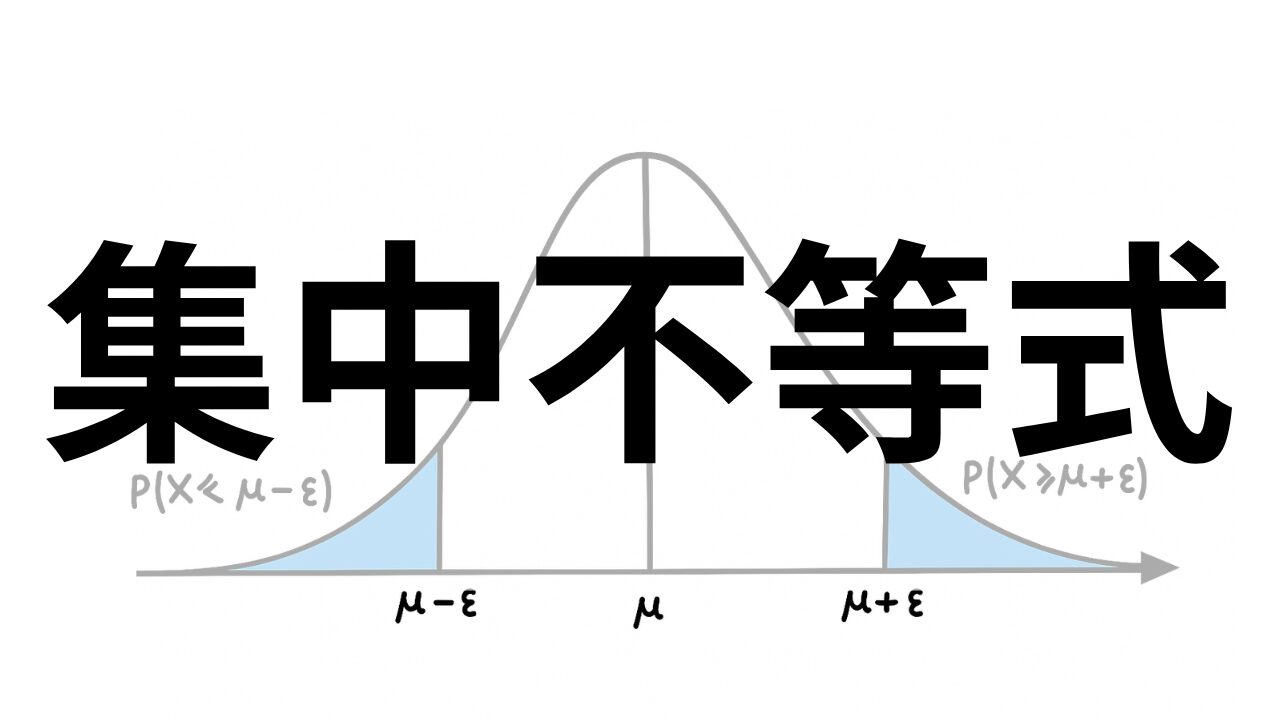
バンディットアルゴリズムで用いる集中不等式【マルコフ、チェビシェフ、ヘフディング】【信頼区間】
皆さんは、「たくさんのサイコロを振って出た目の平均を計算すると、だんだん期待値である3.5に近づいていく」という話を聞いたことがあるかもしれません。これは直感的に正しいように思えますよね。 この記事で学ぶ「測度の集中」とは、まさにこの直感を数学的に厳密に扱うための道具です。特に、機械学習や統計学では、手元にあるデータ(サンプルの集まり)から、まだ見ぬデータ全体(母集団)の性質を推測しようとします。例えば、ある薬の効果を調べるために100人に試した結果から、その薬が日本人全体にどれくらい効くの ...
クイックソート徹底解説-アルゴリズムの仕組みから厳密な性能分析まで
ソートアルゴリズムの世界には、マージソート、ヒープソートなど、数多くの強力な候補が存在します。これらのアルゴリズムは、最悪の場合でも \(\Theta(n \lg n)\) という優れた性能保証を持っています。一方で、今回解説するクイックソートは、最悪のシナリオでは \(\Theta(n^2)\) という、単純なバブルソートなどと同レベルの非常に遅い実行時間となってしまいます。 それにもかかわらず、クイックソートはC言語の標準ライブラリ qsort のような多くの場面で採用され、「実用上最も高速なソートア ...
2分探索木(BST)を完全解説|探索・挿入・削除・計算量・中間順巡回まで
2分探索木(Binary Search Tree;BST)は、動的に変化する要素集合に対して、探索・最小値・最大値・前後要素の取得•挿入•削除といった操作を、木の高さ \(h\) に比例する時間で実現する基本データ構造です。 本章では、BST の定義(2分探索木条件)から始め、中間順木巡回(inorder)による昇順出力、SEARCH/MINIMUM/MAXIMUM/SUCCESSOR/PREDECESSOR の各クエリー、さらに INSERT/DELETE の実装までを、擬似コードとともに ...
乱択アルゴリズム徹底解説:計算量を劇的に改善する「ランダム性」の力
皆さんは「ランダム」という言葉を聞いて、どんなイメージを持つでしょうか?おそらく、サイコロを振る、ルーレットが回る、宝くじを引く、といった予測不能な出来事を思い浮かべるかもしれません。ゲームやギャンブルの世界では、この予測不能性が面白さを生み出す要素となっています。 実は、コンピューターのアルゴリズムの世界でも、「ランダム性」は非常に強力なツールとなり得ます。通常、アルゴリズムはどんな入力に対しても正しい答えを効率的に出すように設計されます。しかし、時には「意地悪な入力」が存在し、特定のアルゴリズムの効率 ...
Transformer完全攻略ロードマップ:基礎から応用までを徹底解説
近年、自然言語処理や画像認識などさまざまな分野で活躍している「Transformer」。その革新的な構造が、深層学習の常識を大きく変えています。しかし、Attentionをはじめとする各要素を正しく理解しないと、実装や応用でつまずくことも多いのではないでしょうか。 本記事では、Transformerを体系的に学ぶために押さえておきたいポイントを4つの記事に分けて、最適な順番で解説した「ロードマップ」をご紹介します。まずはTransformerの全体像を把握し、続けてAttention機構やPosition ...
アルゴリズムの設計:マージソート(Merge-sort)で学ぶ分割統治法の計算量解析
アルゴリズムの設計とは、与えられた問題を解決するための手続き・手順を考案し、それを正しく効率的に実行できるように組み立てる作業のことです。具体的には、入力(問題のデータ)と出力(結果)との間に、どのようなステップを踏めば解が得られるかを体系的に示し、それを計算機(あるいは人間)が順序通りに実行できるように定義することを指します。 アルゴリズムの「性能」を評価するためには、以下のような観点が重要です。 正しさ:アルゴリズムが意図したとおりに動作し、正しい結果を返すかどうか。 実行時間:アルゴリズムを動かした ...
バンディットアルゴリズムで用いる集中不等式【マルコフ、チェビシェフ、ヘフディング】【信頼区間】
皆さんは、「たくさんのサイコロを振って出た目の平均を計算すると、だんだん期待値である3.5に近づいていく」という話を聞いたことがあるかもしれません。これは直感的に正しいように思えますよね。 この記事で学ぶ「測度の集中」とは、まさにこの直感を数学的に厳密に扱うための道具です。特に、機械学習や統計学では、手元にあるデータ(サンプルの集まり)から、まだ見ぬデータ全体(母集団)の性質を推測しようとします。例えば、ある薬の効果を調べるために100人に試した結果から、その薬が日本人全体にどれくらい効くの ...
情報幾何におけるアフィン接続について
皆さん、こんにちは!今日は情報幾何という分野に出てくる「アフィン接続」という考え方を、できるだけ丁寧に解説していきます。 まずは、身近な例から考えてみましょう。例えば、地球儀のような曲面の上に、アリがチョークで線を引くことを想像してみてください。アリにとっての「まっすぐな線」って、どういうものでしょうか? 地球儀の上では、普通の定規で引いたような線は「まっすぐ」ではありませんよね。 実は、この「まっすぐ」という考え方が、アフィン接続と深く関わっているんです。 ベクトル空間と多様体:舞台設定 ...
合コンで分かるホールの結婚定理とその証明
あるところに、これから合コンする予定の男子A,B,Cの3人がいました。 彼らは仲が良く、合コンで狙う女子が被って喧嘩にならないように事前にとある約束をしました。なぜならば合コン中に男子同士で喧嘩するのはみっともないからです。 ある程度場が進んだら、自分の箸を狙っている女子に向け、男子にだけその人が狙っている女の子がわかるようにしました。 そして、その時がやってきました。相対する女子はX,Y,Zの三人 C君はXちゃんに揃えた箸を向けました。 B君は決めかねたのか、Y ...
林(森)な二部グラフで成り立つ不等式について
二部グラフ \(G=(V, U, E)\) が森であるならぱ、 \(|E| \leq|V|+|U|-1\) という不等式が成り立つ理由を説明 します。ここで、森とは閉路を含まないグラフを指します。 まず、基本的なグラフ理論の概念について確認しましょう。 グラフ理論の確認 1. 木と森の定義: ・木: 閉路を持たない連結なグラフ。 ・森: 閉路を持たないグラフ(つまり、複数の木の集合)。 2. 二部グラフ: ・グラフ \(G=(V, U, E)\) が二部グラフである場合、頂点集 ...
テンソル場の定義と性質 リーマン計量とは?
テンソル場を理解するのに必要な知識は、 双対空間(双対基底) テンソル です。 ささっと復習してテンソル場の定義、性質をこの記事で理解します。 この線形空間\(V\)とその双対空間\(V^*\)をそれぞれ\(s\)個、\(r\)個ずつ直積してできるベクトル空間を\((r,s)\)型テンソル空間と呼びます。 テンソル場 多様体\(M\)の各点にテンソルを割り当てたテンソル場というものを考えましょう。 3つ以上のテンソル場のテンソル積も同様です。 &nb ...
ワッサースタイン(Wasserstein)距離とは?距離の公理を満たすことの証明まで
GANなどの生成モデルで使われるようになりたびたび聞くことも増えたワッサースタイン(Wasserstein)距離というものを解説します。 ワッサースタイン距離というのは一言でいうと、確率分布間を測る距離の一つです。 この記事では離散確率分布に対するワッサースタイン距離の定義とそれが距離の公理を満たすことを証明します。 最適輸送問題とは 最適輸送問題は、物理学や経済学などの分野で長い歴史を持つ数理的な問題です。この問題は、ある場所に存在する物資を別の場所に運ぶ際の最適な方法を探求します。具体的 ...
本気で結果を出したい人のための「暗記法」完全マニュアル
※この記事はnoteに公開している「本気で結果を出したい人のための暗記法完全マニュアル」とほぼ同じものです。すでに購入されたことがある方はご注意ください。 まず最初に暗記、すなわちインプットを正確に行うことの爆発力についてご紹介したいと思います。 暗記というと「暗」という字があるだけあって「めんどくさい」などの暗いネガティブなイメージを持ちがちですが 暗記によって得られる効果は絶大です。 それは圧倒的な時間の短縮です。 皆さん経験があると思いますが、「知っている」のと「知らない」のとでは成果とその時間に差 ...
【思い出す】ことが最強の暗記法。知識を頭に叩き込んで忘れないためのコツ【反芻暗記法】
今回は、勉強の基本中の基本であり本質である 「思い出す」ということについて徹底的に掘り下げてみようと思う。 長い長い勉強生活において僕が得た知見をなるべく整理してみるので、勉強で成果を出したいと思っている人は是非一読してもらいたい。 「思い出す」ことが勉強の本質 僕は個人的に「思い出す」という作業が反復・復習の本質だと本気で思っている。 思い出すという作業は、脳に負荷がかかり、脳が苦労して、過去の記憶から思い出したい内容をサルベージしてくることで記憶が強固になっていくのだ &n ...
三浪参考書マニアによる、受験生におすすめの物理参考書・問題集5選
参考書・問題集選びって迷いますよね。 実際僕も悩みに悩んであっちこっちの参考書に手を出しまくっていた時期がありました。 やっていない本があると不安になるんですよね。 ですが、今ならわかります。 物理は特に一冊の参考書をしっかりやった方が成績が上がります。 この記事では皆さんの参考書選びの一助になれるように この経験を踏まえたおすすめの物理の参考書を五つに絞って紹介したいと思います。 ※この記事の内容は全て個人的な所感によるものということをご理解ください 物理の勉強 ...
数学における論理の起点のパターンとその考え方【難関大入試に効果絶大】
先日、こちらの記事のコメントにて 「論理の起点のパターンを見せてほしい」 というご希望があったので、すこし「論理の起点」について深堀りしたいと思います。 たしかに、ただ「論理の起点」「いつ使うか」だけでは、まだ結局どう使えばいいねん。 となってしまうと思われる方もいるかもしれませんので、数学を例に具体例を交えて解説したいと思います 論理の起点とは 論理の起点とは、インプットの際に意識するべき三要素の最終段階 「そのインプットした内容がいつ使えるものなのか」までセットで覚えてしまおうという考え ...
「復習」ってやっぱり勉強において大事という話と具体的な方法を紹介
学校の先生やら塾の講師やらは散々言いますよね 「復習せい」と もう耳タコで、頭では分かっているんです。 ですが、受験が近づくにつれ、勉強する量しなければいけない量が増えていくほど過去の勉強、つまり復習に手が回らなくなりがちで そもそも何回復習すれば良いのか、一定の回数復習しなければいけないとしてそのタイミングをスケジューリングしている時間がそもそももったいなくね??? みたいな悩みってあるあるだと勝手に思ってるんです。 例にもれず僕も散 ...
【モチベーション】受験勉強のやる気を出す方法
いきなりですが やる気の差というのは受験において本当に大きなものです。 皆さんがこれから今以上に学力、偏差値を上げたいのであればモチベーションの維持には細心の注意を払う必要があります。 しかしこの記事を読んでくださっている方の中には という方もいると思います。 実際、私も何度もやる気が出ずらかったことがあります。具体的には ・高校一年、二年のとき ・受験生、浪人生の春と秋 この時期は特に勉強のやる気が出ずらいと思います。この記事を読んでいる方にも心当たりある方もいるかもしれませ ...