2分探索木（BST）を完全解説｜探索・挿入・削除・計算量・中間順巡回まで

2分探索木（Binary Search Tree；BST）は、動的に変化する要素集合に対して、探索・最小値・最大値・前後要素の取得•挿入•削除といった操作を、木の高さ $h$ に比例する時間で実現する基本データ構造です。

本章では、BST の定義（2分探索木条件）から始め、中間順木巡回（inorder）による昇順出力、SEARCH／MINIMUM／MAXIMUM／SUCCESSOR／PREDECESSOR の各クエリー、さらに INSERT／DELETE の実装までを、擬似コードとともに体系的に解説します。平均的にはランダム挿入で高さの期待値が $O(\lg n)$ に収まること、比較モデルに基づく構築の計算量下限など、計算量の背景も丁寧に押さえます。

序論

本章では、計算機科学における基本的なデータ構造の一つである探索木 (Search Tree)、特にその代表例である2分探索木 (Binary Search Tree) について詳述します。
データ構造論において、動的に変化する要素の集合を効率的に管理することは中心的な課題です。ここで言う「動的集合」とは、要素の挿入、削除、検索といった操作が頻繁に行われる集合を指します。探索木は、これらの動的集合操作 (Dynamic-Set Operations)を実現するための強力なデータ構造です。具体的には、以下の操作を提供します。

SEARCH: 特定のキーを持つ要素を集合内から探し出す。
MINIMUM: 集合内で最小のキーを持つ要素を見つける。
MAXIMUM: 集合内で最大のキーを持つ要素を見つける。
PREDECESSOR: 与えられた要素の、キーの順序において直前の要素（先行節点）を見つける。
SUCCESSOR: 与えられた要素の、キーの順序において直後の要素（次節点）を見つける。
INSERT: 新しい要素を集合に加える。
DELETE: 既存の要素を集合から取り除く。

これらの操作を効率的に実行できるため、探索木は辞書 (Dictionary) や優先度付きキュー (Priority Queue) といった、より抽象的なデータ構造の実装基盤として広く利用されます。

2分探索木における上記基本操作の実行時間は、木の高さ (height) に比例するという重要な特性を持ちます。木の高さとは、根 (root) から最も遠い葉 (leaf) までの経路上にある辺の数です。$n$ 個の要素（節点、ノード）を持つ木を考えたとき、その構造によって高さは大きく変動します。

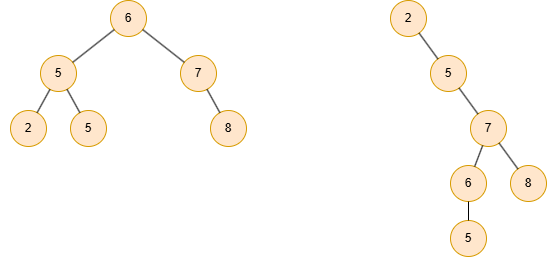
最良の場合: 木が完全2分木 (complete binary tree) に近い形状、すなわち、葉を除くすべての節点が2つの子を持ち、すべての葉がほぼ同じ深さにある場合、その高さは $h = \Theta(\lg n)$ となります。このとき、基本操作の実行時間も $\Theta(\lg n)$ となり、非常に効率的です。
最悪の場合: 木が線形連鎖 (linear chain)、すなわち、各節点が子を一つしか持たず、一直線に連なった形状になる場合、その高さは $h = \Theta(n)$ となります。この場合、基本操作の実行時間は $\Theta(n)$ となり、単純な線形リスト（配列など）を探索するのと同程度の効率しか得られません。

補足

2分探索の計算時間$\Theta(lg n)$は、線形探索の$\Theta(n)$に比べて指数的に高速です。
ただし、2分探索を行うためには、常にデータがソートされている必要がある。そのため、データを追加する際には、適切な位置に追加しなければならず、配列をメンテナンスするためのコストがかかります。
一方、線形探索の場合には、配列中のデータはでたらめに並んでいても構いません。データの追加に気を遣わず、単に最後尾にくっつければよいため、コストがかかりません。
どちらの探索を使うかは、探索と追加のどちらの操作が頻繁に行われるのかを考慮して決めるのが良いでしょう。

このように、2分探索木の性能は、その形状（バランス）に大きく依存します。この問題を解決するため、第13章では木のバランスを動的に維持する2色木、赤黒木 (Red-Black Tree) という改良された2分探索木を学びます。2色木は、木の高さが常に $O(\lg n)$ に保たれることを保証します。

また、ここでは証明を省略しますが、$n$ 個のキーをランダムな順序で挿入して2分探索木を構成した場合、その木の高さの期待値は $O(\lg n)$ となることが知られています。これは、平均的なケースでは2分探索木が良好な性能を示すことを示唆しています。

本章では、まず2分探索木の基本的な定義と性質から始めます。次に、木に格納された値をソートされた順序で出力するための走査（巡回）方法、特定のキーを持つ要素の探索、最小・最大要素の発見、先行・次節点の探索、そして要素の挿入と削除のアルゴリズムについて、順を追って詳細に解説します。

なお、木構造に関する基本的な数学的性質（根、子、親、部分木、深さ、高さなど）については、必要に応じて集合論やグラフ理論の基礎知識を参照してください。

2分探索木（BST）とは？

2分探索木 (Binary Search Tree) は、その名の通り2分木 (Binary Tree) と呼ばれる木構造を基本としています。2分木とは、各節点が最大で2つの子（左の子と右の子）しか持たない木のことです。

データ構造としては、各節点（ノード）はいくつかの属性（フィールド）を持つオブジェクトとして表現されます。

key: 節点に格納される値。このキーを用いて節点の順序が定義されます。
付随データ: キーに関連付けられる情報（ここでは省略します）。
left: 左の子を指すポインタ。左の子が存在しない場合は NIL (null) となります。
right: 右の子を指すポインタ。右の子が存在しない場合は NIL となります。
p: 親を指すポインタ。親が存在しない、つまりその節点が根 (root) である場合は NIL となります。

木全体は、その根節点を指すポインタ（例えば T.root）によって管理されます。木が空の場合、T.root は NIL となります。

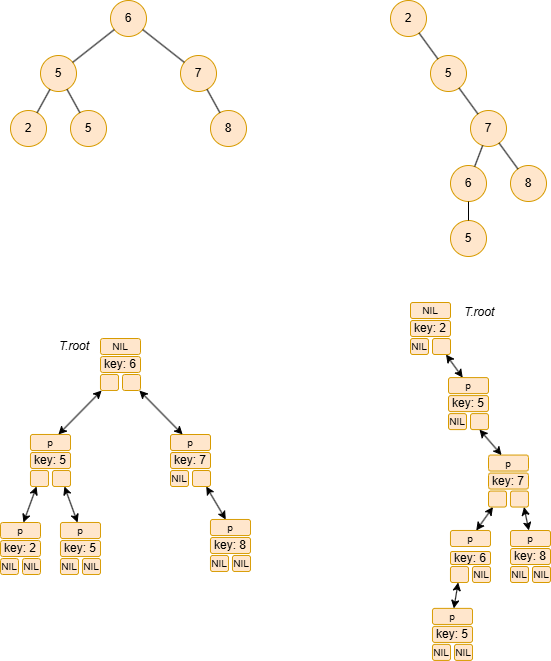
2分探索木条件（binary-search-tree property）

2分探索木が単なる2分木と異なる点は、その節点に格納されるキーが以下の厳密な規則、すなわち 2分探索木条件 (binary-search-tree property) を満たすように配置されていることです。

定義: 2分探索木条件
任意の節点 $x$ を考える。
1. もし節点 $y$ が $x$ の左部分木 (left subtree) に存在するならば、$y.key \le x.key$ が成立する。
2. もし節点 $y$ が $x$ の右部分木 (right subtree) に存在するならば、$y.key \ge x.key$ が成立する。

この条件は、木のすべての節点に対して再帰的に適用されます。

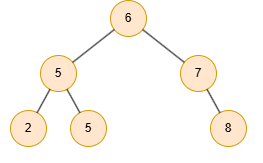
例えば、ある2分探索木を考えます。
根のキーが6であるとします。このとき、2分探索木条件により、根の左部分木に存在するすべてのキーは6以下でなければならず、右部分木に存在するすべてのキーは6以上でなければなりません。例えば、左部分木にはキー {2, 5, 5} が、右部分木にはキー {7, 8} が格納されているとします。
この条件は、左部分木の根（例えばキーが5の節点）に対しても成り立ちます。この節点の左部分木には5以下のキーが、右部分木には5以上のキーが格納されます。

このように、ある節点を基準にすると、その左側にはそれ以下の値が、右側にはそれ以上の値が集まるという構造的な特性が生まれます。この特性こそが、探索操作を効率的に行うための鍵となります。

また、注意すべき点として、同じキーの集合を表現する2分探索木は一意ではありません。キーを挿入する順序によって、異なる構造の木が生成され得ます。例えば、キーの集合 {2, 5, 6, 7, 8} から、高さ2のバランスの取れた木も、高さ4の線形に近い非効率な木も構築可能です。

木の走査（巡回）：中間順・先行順・後行順

2分探索木条件の直接的な帰結として、木に格納されたすべてのキーをソートされた順序で出力（プリント）する簡単なアルゴリズムが存在します。これは中間順木巡回 (inorder tree walk) と呼ばれる再帰的なアルゴリズムです。

中間順木巡回（inorder）の擬似コード


INORDER-TREE-WALK(x)
1 if x ≠ NIL
2     INORDER-TREE-WALK(x.left)
3     print x.key
4     INORDER-TREE-WALK(x.right)

このアルゴリズムを木全体の根 T.root に対して INORDER-TREE-WALK(T.root) として呼び出すことで、木に含まれる全ての要素を昇順に出力できます。

なぜこのアルゴリズムが「中間順」と呼ばれるかというと、根のキー x.key を処理する（ここではプリントする）タイミングが、その左部分木の全てのキーを処理し終えた後であり、かつ右部分木の全てのキーを処理し始める前、すなわち「中間」であるためです。

このアルゴリズムがなぜソート順に出力するのかを、2分探索木条件から証明してみましょう。

証明（数学的帰納法による）:

* 基底: 節点数が0または1の木に対しては、このアルゴリズムが正しくソート順（あるいは単一要素）を出力するのは自明です。
* 帰納的ステップ: 節点数が $k < n$ の任意の木に対してアルゴリズムが正しく動作すると仮定します。節点数 $n$ の木を考え、その根を $x$ とします。
1. アルゴリズムはまず INORDER-TREE-WALK(x.left) を呼び出します。x の左部分木は節点数が $n$ 未満なので、帰納法の仮定により、左部分木に含まれるすべてのキーがソートされた順序で出力されます。2分探索木条件から、これらのキーはすべて x.key 以下です。
2. 次に、アルゴリズムは print x.key を実行します。これにより、左部分木のすべてのキーの次（以上）の値である x.key が出力されます。
3. 最後に、INORDER-TREE-WALK(x.right) を呼び出します。同様に、帰納法の仮定により、右部分木に含まれるすべてのキーがソートされた順序で出力されます。2分探索木条件から、これらのキーはすべて x.key 以上です。
* したがって、出力全体のシーケンスは、( x.key 以下のソート済みキー群) $\rightarrow$ (x.key) $\rightarrow$ (x.key 以上のソート済みキー群) となり、全体としてソートされた順序となります。

参考までに、他の走査方法も紹介します。

先行順木巡回 (preorder tree walk): 根のキーを先に処理し、その後で左部分木、右部分木を再帰的に走査します (print が1行目と2行目の間に来る)。
後行順木巡回 (postorder tree walk): 左部分木、右部分木を再帰的に走査し終えた後で、根のキーを処理します (print が4行目の後に来る)。

計算量解析：INORDER-TREE-WALK は Θ(n)

INORDER-TREE-WALK の実行時間を考えます。このアルゴリズムは、各節点に対して再帰呼び出しを行います。$n$ 個の節点を持つ木において、INORDER-TREE-WALK は各節点に対して何回呼び出されるでしょうか？

各節点 x に対する呼び出し INORDER-TREE-WALK(x) は、x が NIL でない場合にのみ処理が実行されます。x が NIL でない場合、その内部で INORDER-TREE-WALK(x.left) と INORDER-TREE-WALK(x.right) の2つの再帰呼び出しが発生します。

全体の呼び出し回数は、NIL でない節点への呼び出しが $n$ 回、そして各節点からその left および right 子（NIL である場合も含む）への呼び出しが合計 $2n$ 回となります。したがって、総呼び出し回数は $n + 2n = 3n$ 回となり、$O(n)$ です。

各呼び出しにおける処理（NIL チェック、プリント）は定数時間 $O(1)$ で行えるため、アルゴリズム全体の実行時間は $\Theta(n)$ となります。

実行例：INORDER-TREE-WALK の動作軌跡

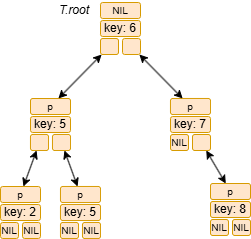
画像の木（根が6）に対して INORDER-TREE-WALK を実行した場合の動作を追跡します。

INORDER-TREE-WALK(6) 呼び出し。
INORDER-TREE-WALK(6.left) → INORDER-TREE-WALK(5) 呼び出し。
INORDER-TREE-WALK(5.left) → INORDER-TREE-WALK(2) 呼び出し。
INORDER-TREE-WALK(2.left) → INORDER-TREE-WALK(NIL) 呼び出し。何もせずリターン。
print 2.key → 出力: 2
INORDER-TREE-WALK(2.right) → INORDER-TREE-WALK(NIL) 呼び出し。何もせずリターン。
INORDER-TREE-WALK(2) 終了。INORDER-TREE-WALK(5) に戻る。
print 5.key → 出力: 5
INORDER-TREE-WALK(5.right) → INORDER-TREE-WALK(5) 呼び出し。
INORDER-TREE-WALK(5.left) → INORDER-TREE-WALK(NIL) 呼び出し。リターン。
print 5.key → 出力: 5
INORDER-TREE-WALK(5.right) → INORDER-TREE-WALK(NIL) 呼び出し。リターン。
INORDER-TREE-WALK(5) 終了。INORDER-TREE-WALK(5) に戻る。
INORDER-TREE-WALK(5) 終了。INORDER-TREE-WALK(6) に戻る。
print 6.key → 出力: 6
INORDER-TREE-WALK(6.right) → INORDER-TREE-WALK(7) 呼び出し。
INORDER-TREE-WALK(7.left) → INORDER-TREE-WALK(NIL) 呼び出し。リターン。
print 7.key → 出力: 7
INORDER-TREE-WALK(7.right) → INORDER-TREE-WALK(8) 呼び出し。
INORDER-TREE-WALK(8.left) → INORDER-TREE-WALK(NIL) 呼び出し。リターン。
print 8.key → 出力: 8
INORDER-TREE-WALK(8.right) → INORDER-TREE-WALK(NIL) 呼び出し。リターン。
INORDER-TREE-WALK(8) 終了。INORDER-TREE-WALK(7) に戻る。
INORDER-TREE-WALK(7) 終了。INORDER-TREE-WALK(6) に戻る。
INORDER-TREE-WALK(6) 終了。

最終的な出力は 2, 5, 5, 6, 7, 8 となり、ソートされた順序であることが確認できます。

2分探索木構築の計算量下限

命題

比較演算のみを用いる任意のアルゴリズムが、$n$ 個の要素からなるリストから2分探索木を構築するには、最悪の場合 $\Omega(n \lg n)$ 時間を要する。

証明:
この証明は、比較ソートの計算量下限を利用した背理法によります。

仮定: $n$ 個の要素を持つ任意のリストから、最悪実行時間 $o(n \lg n)$ で2分探索木を構築するアルゴリズム BUILD-BST が存在すると仮定します。（$o(n \lg n)$ は、$n \lg n$ よりも漸近的に小さい任意の関数を表します。）
ソートアルゴリズムの構築: この仮定上のアルゴリズム BUILD-BST を用いて、新しいソートアルゴリズム BST-SORT を以下のように構築します。

* Step 1: 与えられた $n$ 個の要素のリストを入力として、BUILD-BST を呼び出し、2分探索木 $T$ を構築する。仮定より、このステップの実行時間は最悪でも $o(n \lg n)$ です。
* Step 2: 構築された木 $T$ に対して、INORDER-TREE-WALK を実行し、キーを順に出力する。前述の通り、このステップの実行時間は $\Theta(n)$ です。

全体の実行時間: BST-SORT の全体の実行時間は、Step 1 と Step 2 の実行時間の和となります。

$T(n) = o(n \lg n) + \Theta(n)$
漸近記法の定義から、これは $o(n \lg n)$ となります。

矛盾: BST-SORT は、要素間の比較のみを用いて（BUILD-BST が比較に基づくと考えられるため）$n$ 個の要素をソートするアルゴリズムです。しかし、比較ソートの決定木モデルから、任意の比較ソートアルゴリズムは最悪の場合において $\Omega(n \lg n)$ 回の比較が必要であることが証明されています。したがって、最悪実行時間が $o(n \lg n)$ である比較ソートアルゴリズムは存在し得ません。
結論: Step 3 の結果は Step 4 の事実と矛盾します。この矛盾は、最初の仮定、すなわち「最悪実行時間 $o(n \lg n)$ で2分探索木を構築するアルゴリズムが存在する」という仮定が誤っていたことに起因します。

したがって、比較演算のみを用いて2分探索木を構築するアルゴリズムは、最悪の場合 $\Omega(n \lg n)$ の時間を要することが証明されました。

基本クエリー：SEARCH／MINIMUM／MAXIMUM／SUCCESSOR／PREDECESSOR

2分探索木はその構造的特性から、データの検索や順序に関する問い合わせ、すなわちクエリー (query) 操作を非常に効率的に実行できます。本節では、SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR といった基本的なクエリー操作を検討し、これらの操作がすべて木の高さ $h$ に比例する時間、すなわち $O(h)$ で実行できることを示します。

探索（TREE-SEARCH／ITERATIVE-TREE-SEARCH）

与えられたキー $k$ を持つ節点を木の中から探し出す操作は、2分探索木の最も基本的な操作です。

再帰的な探索アルゴリズム


TREE-SEARCH(x, k)
1 if x == NIL or k == x.key
2     return x
3 if k < x.key
4     return TREE-SEARCH(x.left, k)
5 else return TREE-SEARCH(x.right, k)

この手続き TREE-SEARCH(x, k) は、節点 x を根とする部分木の中からキー $k$ を持つ節点を探索します。木全体を探索するには、TREE-SEARCH(T.root, k) を呼び出します。

アルゴリズムの動作原理:

基底ケース (終了条件):

* x が NIL の場合、探索している部分木が空であることを意味し、キー $k$ は存在しません。NIL を返します。
* k == x.key の場合、目的の節点が見つかったので、その節点 x へのポインタを返します。

再帰ステップ:

* k < x.key の場合: 2分探索木条件により、キー $k$ が存在するとすれば、それは x の左部分木にしかあり得ません。なぜなら、右部分木のキーはすべて x.key 以上だからです。したがって、探索範囲を左部分木に限定し、TREE-SEARCH(x.left, k) を再帰的に呼び出します。
* k > x.key の場合: 同様に、キー $k$ は x の右部分木にしか存在し得ません。探索範囲を右部分木に限定し、TREE-SEARCH(x.right, k) を再帰的に呼び出します。

このアルゴリズムがたどる経路は、根から始まり、各ステップで左か右の子へと下っていく一本の単純路 (simple path) となります。したがって、最悪の場合でも、たどる節点の数は木の高さ $h$ を超えません。各節点での処理は定数時間であるため、TREE-SEARCH の実行時間は $O(h)$ となります。

反復的な探索アルゴリズム

TREE-SEARCH の再帰呼び出しは、手続きの最後に現れる末尾再帰 (tail recursion) の形をしています。このような再帰は、単純なループ構造に展開することができ、多くの場合、関数呼び出しのオーバーヘッドがなくなるため、より高速に動作します。


ITERATIVE-TREE-SEARCH(x, k)
1 while x ≠ NIL and k ≠ x.key
2     if k < x.key
3         x = x.left
4     else x = x.right
5 return x

この反復版は、ポインタ x を根から順に木の下方へ移動させながら、キー $k$ を持つ節点を探します。ループは、x が NIL になる（探索失敗）か、k == x.key となる（探索成功）まで続きます。こちらも実行時間は $O(h)$ です。

最小値・最大値（TREE-MINIMUM／TREE-MAXIMUM）

2分探索木条件から、最小値や最大値を持つ要素は木の特定の位置に存在することが保証されます。

最小値

TREE-MINIMUM(x): 節点 x を根とする部分木の中で、最小のキーを持つ節点を返します。

直感的理解: 2分探索木では、ある節点よりも小さいキーはすべてその左部分木に存在します。この論理を繰り返し適用すると、最も小さいキーを持つ節点は、根から始まって左の子ポインタ left をたどり続け、それ以上左に進めなくなった場所にあるはずです。


TREE-MINIMUM(x)
1 while x.left ≠ NIL
2     x = x.left
3 return x

この手続きは、x.left が NIL になるまで x を x.left で更新し続けます。ループが終了した時点の x が、最小のキーを持つ節点となります。

正当性の証明:
節点 $x$ を根とする部分木を考えます。

もし $x$ が左の子を持たない場合、$x$ の左部分木は空です。右部分木のキーはすべて $x.key$ 以上なので、この部分木における最小キーは $x.key$ です。アルゴリズムはループに入らずに $x$ を返すので正しいです。
もし $x$ が左の子を持つ場合、2分探索木条件から、部分木内の最小キーは $x$ 自身やその右部分木には存在せず、必ず左部分木内に存在します。したがって、探索を左部分木に移す x = x.left は正当です。このプロセスを繰り返すことで、最終的に左の子を持たない節点に到達し、それが部分木全体の最小値となります。

最大値

TREE-MAXIMUM(x): 節点 x を根とする部分木の中で、最大のキーを持つ節点を返します。

最小値の探索と完全に対称的な操作です。最大のキーを持つ節点は、根から右の子ポインタ right をたどり続けた終点に存在します。


TREE-MAXIMUM(x)
1 while x.right ≠ NIL
2     x = x.right
3 return x

TREE-MINIMUM と TREE-MAXIMUM の両手続きは、根から葉に向かう単純路をたどるため、木の高さが $h$ のとき、実行時間は $O(h)$ となります。

次節点・先行節点（TREE-SUCCESSOR／TREE-PREDECESSOR）

ソートされたキーの順序において、ある節点 $x$ の次にくる要素、すなわち次節点 (successor) を見つける操作も重要です。キーがすべて異なると仮定すれば、これは「$x.key$ より大きいキーの中で、最小のキーを持つ節点」を指します。キーに重複がある場合も含め、より厳密には「中間順木巡回で $x$ の次に訪問される節点」と定義します。

TREE-SUCCESSOR(x) は、この次節点を探索する手続きです。探索は2つの場合に分けられます。


TREE-SUCCESSOR(x)
1 if x.right ≠ NIL
2     return TREE-MINIMUM(x.right)
3 y = x.p
4 while y ≠ NIL and x == y.right
5     x = y
6     y = y.p
7 return y

アルゴリズムの動作原理:

ケース 1: x が右部分木を持つ場合 (第1-2行)

x.key よりも大きいキーは、すべて x の右部分木か、x の祖先に存在します。このうち、x に最も近い（値が小さい）のは、x の右部分木に存在するキーです。その中でも最小のキーを持つ節点が x の次節点となります。したがって、x の右部分木の最小要素、すなわち TREE-MINIMUM(x.right) が求める次節点です。

ケース 2: x が右部分木を持たない場合 (第3-7行)

この場合、x よりも大きいキーは x の子孫には存在しません。したがって、次節点は x の祖先の中に存在する必要があります。
では、どの祖先が次節点になるのでしょうか？
x から親ポインタ p をたどって木を上っていきます。もし、現在注目している節点（最初は x）がその親の右の子であるならば、その親のキーは現在注目している節点のキーよりも小さいです。つまり、まだ次節点には出会っていません。そこで、さらに親をたどります。
このプロセスを繰り返し、初めて現在注目している節点 x がその親 y の左の子になった瞬間を考えます。これは、x が y の左部分木に属していることを意味し、中間順木巡回では y の左部分木をすべて訪問した後に y を訪問します。したがって、この y こそが x の次節点となります。
アルゴリズムの第4-6行の while ループは、まさにこの「自分が親の左の子になるまで、木を遡る」操作を実装しています。

TREE-PREDECESSOR(x) (先行節点) の探索は、TREE-SUCCESSOR と完全に対称的なアルゴリズムで実現できます。
どちらの手続きも、木を上または下に向かう単純路をたどるため、実行時間は $O(h)$ です。

以上の議論をまとめると、次の定理が成り立ちます。

定理

動的集合演算 SEARCH, MINIMUM, MAXIMUM, SUCCESSOR, PREDECESSOR は、高さ $h$ の2分探索木上で $O(h)$ 時間で動作するように実現できる。

補足解説

子を2つ持つ節点の次節点と先行節点

命題: 2分探索木の節点 $x$ が子を2つ持つならば、
(a) その次節点 $y$ は左の子を持たない。
(b) その先行節点 $z$ は右の子を持たない。

証明:
(a) $x$ が子を2つ持つ場合、その次節点 $y$ は TREE-SUCCESSOR のアルゴリズム（ケース1）により、$x$ の右部分木の最小要素となります。すなわち、$y = \text{TREE-MINIMUM}(x.right)$ です。
TREE-MINIMUM の定義により、ある部分木の最小要素を持つ節点は、その部分木内で最も左に位置する節点です。もし節点 $y$ が左の子 $y.left$ を持つと仮定すると、$y.left.key \le y.key$ となり、$y$ が最小要素であることに矛盾します（$y.left$ の方が小さいか等しく、より左にあるため）。したがって、次節点 $y$ は左の子を持ちません。

(b) 証明は (a) と対称的です。$x$ の先行節点 $z$ は、$x$ の左部分木の最大要素となります。すなわち、$z = \text{TREE-MAXIMUM}(x.left)$ です。もし節点 $z$ が右の子 $z.right$ を持つと仮定すると、$z.right.key \ge z.key$ となり、$z$ が最大要素であることに矛盾します。したがって、先行節点 $z$ は右の子を持ちません。

挿入と削除

これまでは静的な木に対するクエリー操作を見てきましたが、本節では動的集合の核となる操作、すなわち要素の挿入 (Insertion) と削除 (Deletion) を扱います。これらの操作は、木構造を変更しますが、その過程で2分探索木条件が常に維持されるように注意深く設計されなければなりません。

挿入（TREE-INSERT）

新しい節点 $z$ を2分探索木 $T$ に挿入するには、手続き TREE-INSERT を用います。この手続きは、木 $T$ と、挿入する節点 $z$ を引数に取ります。$z$ は事前に z.key に値が設定され、z.left = NIL, z.right = NIL と初期化されているものとします。


TREE-INSERT(T, z)
 1  y = NIL
 2  x = T.root
 3  while x ≠ NIL
 4      y = x
 5      if z.key < x.key
 6          x = x.left
 7      else x = x.right
 8  z.p = y
 9  if y == NIL
10      T.root = z             // 木 T は空であった
11  elseif z.key < y.key
12      y.left = z
13  else y.right = z

アルゴリズムの動作原理:

TREE-INSERT は、新しい節点 $z$ を挿入すべき適切な場所（葉として接続できる場所）を探し出し、そこに接続する、という2段階の処理を行います。

挿入位置の探索 (第1-7行):

この部分は ITERATIVE-TREE-SEARCH と非常によく似ています。ポインタ x を木の根から始め、z.key と x.key を比較しながら木を下っていきます。
* z.key < x.key ならば左へ (x = x.left)
* z.key >= x.key ならば右へ (x = x.right)
この探索と同時に、x の一歩後ろを追いかける追従ポインタ (trailing pointer) y を維持します (y = x)。y は常に x の親を指すことになります。
while ループは、x が NIL になったときに終了します。このとき、x が指していた NIL こそが、節点 z が接続されるべき場所であり、その親はポインタ y が指す節点となります。

節点の接続 (第8-13行):

探索が完了した時点で、y は挿入される z の親となる節点を指しています（木が空だった場合を除く）。
* z.p = y (第8行): まず、z の親ポインタを y に設定します。
* 次に、y の子ポインタ（left または right）を z に設定する必要があります。
* y == NIL (第9-10行): このケースは、ループが一度も実行されなかった、つまり木が最初から空 (T.root == NIL) であった場合にのみ発生します。このとき、z は新しい根となります。
* z.key < y.key (第11-12行): z のキーが親 y のキーより小さい場合、z は y の左の子として接続されます。
* z.key >= y.key (第13行): そうでない場合、z は y の右の子として接続されます。

このアルゴリズムがたどる経路は、根から新しい葉までの単純路です。したがって、高さ $h$ の木に対する TREE-INSERT の実行時間は $O(h)$ となります。

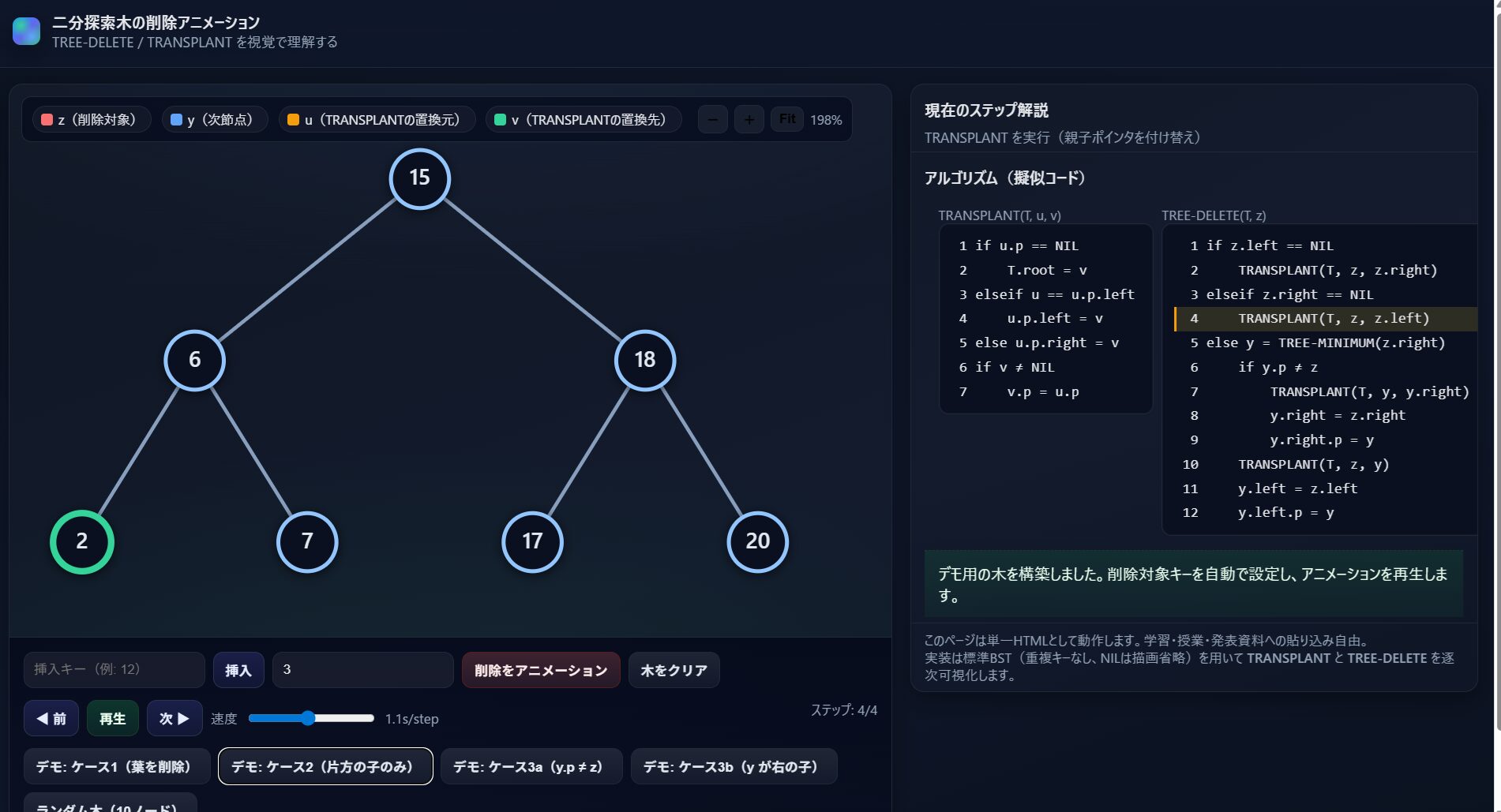
削除（TRANSPLANT／TREE-DELETE）

節点の削除は、挿入よりも場合分けが複雑になります。削除操作は、削除対象の節点 $z$ が持つ子の数によって、大きく3つのケースに分類されます。

$z$ が子を持たない（葉である）場合: $z$ を単純に木から取り除き、その親の子ポインタを NIL に設定します。
$z$ が子を1つだけ持つ場合: $z$ を木から取り除き、$z$ の唯一の子を、$z$ がもともといた位置に「持ち上げ」て、その親と接続します。
$z$ が子を2つ持つ場合: これが最も複雑なケースです。

* $z$ を直接取り除くことはできません。なぜなら、2つの子をどちらも $z$ の親に直接つなぐことはできないからです（親は子を2つまでしか持てない）。
* そこで、$z$ の次節点 (successor) y を見つけます。y は $z$ の右部分木に存在し、かつ左の子を持ちません（先の補足）。
* この y を使って $z$ を置き換える、という戦略を取ります。具体的には、y をその現在の位置から取り除き、$z$ があった位置に移動させます。
* y を移動させた後、$y$ の右の子（もしあれば）や、$z$ の元の子とのポインタを適切に再設定する必要があります。

この削除ロジックを実装するために、まず部分木を別の部分木で置き換えるヘルパー手続き TRANSPLANT を導入します。

ヘルパー手続き `TRANSPLANT`

TRANSPLANT(T, u, v) は、節点 u を根とする部分木を、節点 v を根とする部分木で置き換える操作を行います。具体的には、u の親 u.p が、u の代わりに v を子として持つようにポインタを更新し、同時に v の親ポインタも u.p に設定します。


TRANSPLANT(T, u, v)
1 if u.p == NIL
2     T.root = v
3 elseif u == u.p.left
4     u.p.left = v
5 else u.p.right = v
6 if v ≠ NIL
7     v.p = u.p

動作解説:

第1-2行: u が木の根である場合。置き換え後の根は v となります。
第3-5行: u が根でない場合。u がその親の左の子か右の子かを判断し、親の子ポインタを v に向け替えます。
第6-7行: v が NIL でない場合、v の親ポインタを u の親に設定します。

重要な注意点: TRANSPLANT は v の子ポインタ (v.left, v.right) には関与しません。これらの更新は、TRANSPLANT を呼び出す側の責任となります。

削除手続き `TREE-DELETE`

TRANSPLANT を用いて、節点 $z$ を削除する手続き TREE-DELETE を実装します。


TREE-DELETE(T, z)
 1 if z.left == NIL
 2     TRANSPLANT(T, z, z.right)      // zをその右の子で置き換える
 3 elseif z.right == NIL
 4     TRANSPLANT(T, z, z.left)       // zをその左の子で置き換える
 5 else y = TREE-MINIMUM(z.right)     // yはzの次節点
 6     if y.p ≠ z
 7         TRANSPLANT(T, y, y.right)
 8         y.right = z.right
 9         y.right.p = y
10     TRANSPLANT(T, z, y)
11     y.left = z.left
12     y.left.p = y

アルゴリズムの動作解説:

ケース 1: z が左の子を持たない (第1-2行)

この場合、$z$ をその右の子で置き換えます。z の右の子が NIL であっても（つまり z が葉であっても）この処理は正しく機能し、z は NIL で置き換えられます。これは前述の「子が0個」と「子が1個（右の子のみ）」の両方の場合をカバーします。

ケース 2: z が右の子を持たない（が、左の子は持つ）(第3-4行)

if が偽で elseif が真なので、z.left ≠ NIL かつ z.right == NIL です。この場合、$z$ をその左の子で置き換えます。これは「子が1個（左の子のみ）」の場合に対応します。

ケース 3: z が2つの子を持つ (第5-12行)

ここが最も複雑な部分です。
1. 次節点の特定 (第5行): まず、$z$ の次節点 y を見つけます。これは $z$ の右部分木の最小要素です。
2. y の位置に応じた処理: y が $z$ の直接の右の子であるか否かで、処理が少し異なります。
* サブケース 3a: y が z の右の子ではない場合 (第6-9行)
この場合、y は $z$ の右部分木のもっと深い位置にあります。

- Step 1 (第7行): y を現在の位置から取り除く必要があります。y は次節点（右部分木の最小値）なので左の子を持ちません。したがって、y をその右の子で置き換えます (TRANSPLANT(T, y, y.right))。
- Step 2 (第8-9行): y が $z$ の右部分木を引き継ぐ準備をします。y の右の子を $z$ の右の子に設定し、その親ポインタも更新します (y.right = z.right, y.right.p = y)。
* サブケース 3b: y が z の直接の右の子である場合 (第6行の if が偽)

この場合、第7-9行はスキップされます。y は既に $z$ の右の子なので、y を移動させるための特別な処理は不要です。y の右部分木はそのまま維持されます。
3. z を y で置き換える (第10-12行):
上記どちらのサブケースの後でも、最終的に $z$ があった場所を y で置き換えます。
- Step 3 (第10行): z を y で置き換えます (TRANSPLANT(T, z, y))。この時点で、y は $z$ の親と正しく接続されます。
- Step 4 (第11-12行): y が $z$ の左部分木を引き継ぎます。y の左の子を $z$ の左の子に設定し、その親ポインタも更新します (y.left = z.left, y.left.p = y)。

イメージしやすくしてもらうために、2分探索木の削除のアルゴリズムの流れを見ることができるアニメーションページを作成してきました。併せてみるとわかりやすいと思います。

https://www.nomuyu.com/wp-content/uploads/2025/08/bst_delete_animation.html

この手続きは、TREE-MINIMUM の呼び出し（$O(h)$）と、定数回の TRANSPLANT 呼び出し（各 $O(1)$）から構成されるため、全体の実行時間は高さ $h$ の木に対して $O(h)$ となります。

以上の結果を定理としてまとめます。

定理

動的集合演算 INSERT と DELETE は、高さ $h$ の2分探索木上で $O(h)$ 時間で動作するように実現できる。

ランダム BST の平均解析とクイックソートとの対応

ランダムに構成した2分探索木

この問題は、ランダムにキーを挿入して作られた2分探索木の平均的な性質を解析するもので、乱択クイックソートの解析との興味深い関連性を示唆しています。

a. 節点の深さの平均
節点 $x$ の根からの深さを $d(x, T)$ とします。木の総経路長 (total path length) $P(T)$ は、全節点の深さの和と定義されます:
$P(T) = \sum_{x \in T} d(x, T)$
$n$ 個の節点を持つ木 $T$ における、節点の深さの平均は、定義より
$\frac{1}{n} \sum_{x \in T} d(x, T) = \frac{1}{n} P(T)$
となります。したがって、$P(T)$ の期待値が $O(n \lg n)$ であることを示せば、深さの平均の期待値が $O(\lg n)$ であることが示されます。

b. 総経路長の漸化式
木 $T$ の根を $r$、その左部分木を $T_L$、右部分木を $T_R$ とします。$T_L$ に属する任意の節点 $x$ を考えます。$x$ の $T_L$ における深さを $d(x, T_L)$ とすると、$T$ における深さは、根 $r$ を経由するため1だけ増加し、$d(x, T) = d(x, T_L) + 1$ となります。同様に、$T_R$ に属する節点 $y$ についても $d(y, T) = d(y, T_R) + 1$ です。
根 $r$ の深さは $d(r, T) = 0$ です。
$T_L$ の節点数を $|T_L|$、$T_R$ の節点数を $|T_R|$ とすると、
$P(T) = \sum_{x \in T} d(x, T) = d(r, T) + \sum_{x \in T_L} d(x, T) + \sum_{y \in T_R} d(y, T)$
$P(T) = 0 + \sum_{x \in T_L} (d(x, T_L) + 1) + \sum_{y \in T_R} (d(y, T_R) + 1)$
$P(T) = \left(\sum_{x \in T_L} d(x, T_L)\right) + \sum_{x \in T_L} 1 + \left(\sum_{y \in T_R} d(y, T_R)\right) + \sum_{y \in T_R} 1$
$P(T) = P(T_L) + |T_L| + P(T_R) + |T_R|$
$|T_L| + |T_R| = n-1$ なので、
$P(T) = P(T_L) + P(T_R) + n - 1$
が成り立ちます。

c.総経路長の期待値の漸化式
条件付き平均 $\mathbb{E}[P(T)\mid A_i]$ を計算

根が $k_{i+1}$ に決まる（= $A_i$）と、

左部分木 $T_L$ は大きさ $i$ のランダム BST
右部分木 $T_R$ は大きさ $n-i-1$ のランダム BST

どんな BST にも成り立つ恒等式
$$
P(T)=P(T_L)+P(T_R)+(n-1)
$$
（根以外の $n-1$ 個の深さが +1 されるぶん）に、条件付き期待値をとると
$$
\mathbb{E}[P(T)\mid A_i] =\mathbb{E}[P(T_L)\mid A_i]+\mathbb{E}[P(T_R)\mid A_i]+(n-1).
$$
ここで
$$
\mathbb{E}[P(T_L)\mid A_i]=P(i),\qquad
\mathbb{E}[P(T_R)\mid A_i]=P(n-i-1)
$$
（理由：根を固定しても左右に入るキーの“相対順”は等確率のままなので、それぞれ「サイズ $i$」「サイズ $n-i-1$」のランダム BST と同じ分布 ⇒ その平均は定義どおり $P(i),\,P(n-i-1)$）。
ゆえに
$$
\mathbb{E}[P(T)\mid A_i]=P(i)+P(n-i-1)+(n-1).
$$

全期待値の法則で平均化

$$
\mathbb{E}[P(T)]=\sum_{i=0}^{n-1}\Pr(A_i)\,\mathbb{E}[P(T)\mid A_i] =\frac{1}{n}\sum_{i=0}^{n-1}\Bigl(P(i)+P(n-i-1)+(n-1)\Bigr).
$$
したがって
$$
P(n)=\frac{1}{n}\sum_{i=0}^{n-1}\Bigl(P(i)+P(n-i-1)+(n-1)\Bigr).
$$

d.漸化式の変形（シグマの整理）

項を分解

$$
P(n)=\frac{1}{n}\left(\sum_{i=0}^{n-1}P(i)\;+\;\sum_{i=0}^{n-1}P(n-i-1)\;+\;\sum_{i=0}^{n-1}(n-1)\right).
$$

添字の入れ替え（リネーム）

$\sum_{i=0}^{n-1}P(n-i-1)$ は $k=n-i-1$ と置けば $k$ は $n-1,\dots,0$ を動く。順序は関係ないので
$$
\sum_{i=0}^{n-1}P(n-i-1)=\sum_{k=0}^{n-1}P(k).
$$
よって
$$
\sum_{i=0}^{n-1}P(i)+\sum_{i=0}^{n-1}P(n-i-1)
=2\sum_{k=0}^{n-1}P(k).
$$

定数の和（ここがつまずきポイント）

$$
\mathbb{E}[P(T)\mid A_i] =\mathbb{E}[P(T_L)\mid A_i]+\mathbb{E}[P(T_R)\mid A_i]+(n-1).
$$

まとめ

$$
\mathbb{E}[P(T)\mid A_i] =\mathbb{E}[P(T_L)\mid A_i]+\mathbb{E}[P(T_R)\mid A_i]+(n-1).
$$
さらに $P(0)=0$ なので 0 項は消え、
$$
\mathbb{E}[P(T)\mid A_i] =\mathbb{E}[P(T_L)\mid A_i]+\mathbb{E}[P(T_R)\mid A_i]+(n-1).
$$
漸近評価では $(n-1)=\Theta(n)$ と書いてもよい（以降の解析で $O(n\lg n)$ を導く際に用いる）。

e. 漸化式の解
この漸化式 $P(n) = \frac{2}{n} \sum_{k=1}^{n-1} P(k) + \Theta(n)$ は、乱択クイックソートの期待比較回数の漸化式と全く同じ形をしています。この形式の漸化式の解は $O(n \lg n)$ であることが知られています（置換法や、漸化式を変形して調和級数に帰着させることで証明可能）。
したがって、$P(n) = O(n \lg n)$ と結論付けられます。
これにより、a. の議論から、ランダムに構成された2分探索木の節点の深さの期待平均は $\frac{1}{n}P(n) = \frac{1}{n} O(n \lg n) = O(\lg n)$ となります。

f. クイックソートとの対応
乱択クイックソートと2分探索木構築の間の比較操作の対応付けは以下の通りです。

クイックソート: 配列 $A[p..r]$ をソートする際、ランダムにピボット $x=A[q]$ を選びます。その後、他のすべての要素 $A[i]$ ($i \neq q$) を $x$ と比較し、$A[i] < x$ なら左側のパーティションへ、$A[i] \ge x$ なら右側のパーティションへ分割します。このプロセスを再帰的に繰り返します。
2分探索木: $n$ 個のキーをランダムな順序で挿入します。最初に挿入されたキーが木の根になります。次に挿入されるキーは、根のキーと比較され、小さければ左部分木へ、大きければ右部分木へと進みます。このプロセスが再帰的に繰り返されます。

両者の対応:

最初に挿入されるキー（木の根）は、クイックソートの最初のピボットに対応します。
あるキーを木に挿入する際にたどる経路上の各節点との比較は、クイックソートにおいてある要素が複数の再帰レベルでピボットと比較されることに対応します。
ある要素 $u$ と $v$ が比較されるのは、一方がもう一方の祖先である場合に限られます。これはクイックソートでも同様で、$u$ と $v$ が比較されるのは、一方がピボットとして選ばれ、もう一方がそのピボットが含まれるパーティション内に存在する場合に限られます。

したがって、クイックソートのピボット選択順序を、2分探索木へのキーの挿入順序と一致させることで、両者が行う比較の集合（どの要素ペアが比較されるか）は完全に同一になります。ただし、比較が行われるタイミングや順序は異なる場合があります。