クイックソート徹底解説-アルゴリズムの仕組みから厳密な性能分析まで

ソートアルゴリズムの世界には、マージソート、ヒープソートなど、数多くの強力な候補が存在します。これらのアルゴリズムは、最悪の場合でも \(\Theta(n \lg n)\) という優れた性能保証を持っています。一方で、今回解説するクイックソートは、最悪のシナリオでは \(\Theta(n^2)\) という、単純なバブルソートなどと同レベルの非常に遅い実行時間となってしまいます。

それにもかかわらず、クイックソートはC言語の標準ライブラリ qsort のような多くの場面で採用され、「実用上最も高速なソートアルゴリズム」という名声をほしいままにしています。この一見矛盾した評価はどこから来るのでしょうか？

その答えは、クイックソートの驚異的な平均性能にあります。クイックソートは、平均的には \(\Theta(n \lg n)\) で動作し、さらにこのオーダー記法に隠された定数倍のコストが他のアルゴリズムに比べて非常に小さいのです。また、追加のメモリをほとんど必要としないインプレース（in-place）なアルゴリズムであること、そしてキャッシュメモリを効率的に利用できる構造であることも、その実用的な速さに貢献しています。

この記事では、クイックソートの謎を解き明かしていきます。この記事を読み終える頃には、なぜクイックソートがこれほどまでに重要視されるのか、その真の理由を深く理解できるはずです。

本記事の構成は以下の通りです。

クイックソートの基本アルゴリズム

クイックソートは、分割統治法 (Divide-and-Conquer) というアルゴリズム設計の強力なパラダイムに基づいています。これは、複雑な問題をより小さな、扱いやすい部分問題に分割し、それぞれを解決してから、その結果を統合して元の問題を解決する手法です。

分割統治法は、多くの有効なアルゴリズムの構築に使われる再帰的な設計手法で、「分割」「統治」「結合」の３つのステップを踏むのが一般的です。

分割統治法によるアプローチ

クイックソートが配列 A の部分配列 A[p...r] をソートするプロセスは、以下の3つのステップで構成されます。まずは概観だけ掴んでください

分割 (Divide):

配列 A[p...r] 内から一つの要素をピボット (pivot) として選びます。そして、このピボットを基準にして、配列を2つの部分配列 A[p...q-1] と A[q+1...r] に再配置します。この操作（パーティショニングと呼ばれます）が終わると、以下の状態が満たされます。

• A[p...q-1] に含まれるすべての要素は、ピボット A[q] 以下である。
• A[q+1...r] に含まれるすべての要素は、ピボット A[q] 以上である。

この過程で、ピボットが最終的に配置されたインデックス q が決まります。

統治 (Conquer):

分割された2つの部分配列 A[p...q-1] と A[q+1...r] に対して、クイックソートを再帰的に呼び出して、それぞれをソートします。

結合 (Combine):

何もしません！

これがクイックソートの美しい特徴です。分割のステップで、部分配列間の大小関係は既に確定しています（A[p...q-1] の要素 ≤ A[q] ≤ A[q+1...r] の要素）。したがって、2つの部分配列がそれぞれソートされれば、配列全体も自動的にソートされた状態になります。

この「結合」ステップが不要であるため、マージソートのように結果をマージするための追加の処理やメモリ領域が必要ありません。

QUICKSORT プロシージャ

この分割統治法を実装したのが QUICKSORT プロシージャです。配列全体 A[1...n] をソートするには、QUICKSORT(A, 1, n) を呼び出します。

QUICKSORT(A, p, r)
1  if p < r
2      // 分割：A[p...r]をピボットA[q]の周りで分割する
3      q = PARTITION(A, p, r)
4      // 統治：2つの部分配列を再帰的にソートする
5      QUICKSORT(A, p, q - 1)
6      QUICKSORT(A, q + 1, r)

• 1行目: p < r は、部分配列に要素が2つ以上存在するかをチェックする再帰のベースケースです。要素が1つ以下（p >= r）なら、その部分配列は既にソート済みなので、何もしません。
• 3行目: アルゴリズムの核心である PARTITION プロシージャを呼び出し、分割後のピボットのインデックス q を受け取ります。
• 5-6行目: ピボットを除いた左右の部分配列に対して、QUICKSORT を再帰的に呼び出します。

核心部: PARTITION プロシージャ

クイックソートの性能と正しさは、この PARTITION プロシージャにすべてかかっています。ここでは、Nico Lomutoによる一般的な実装（Lomutoパーティションスキーム）を見ていきましょう。このプロシージャは、部分配列の最後の要素 A[r] をピボットとして選択します。

PARTITION(A, p, r)
1  x = A[r]          // ピボットとして最後の要素を選択
2  i = p - 1         // iは「x以下の要素グループ」の末尾を指す
3  for j = p to r - 1
4      if A[j] <= x
5          i = i + 1
6          exchange A[i] with A[j]
7  // ピボットを正しい位置に移動
8  exchange A[i + 1] with A[r]
9  return i + 1      // ピボットの最終的なインデックスを返す

非常にイメージしやすく、理解の助けになる動画があるので、是非見てください。

緑色の丸がここでのjでオレンジ色の丸がiです。

Lumotoパーティションの動画

PARTITION プロシージャの正当性の証明

アルゴリズムが常に正しく動作することを保証するには、数学的な証明が必要です。ここでは、ループ不変条件 (Loop Invariant) を用いて PARTITION の正しさを証明します。ループ不変条件とは、ループの各反復の開始時点（および終了後）で常に真となる条件式のことです。

この不変条件が真であることを、3つのステップ（初期化、維持、終了）で証明します。

初期化 (Initialization):

ループの最初の反復が始まる直前（j=p）の状態を考えます。このとき、2行目で i は p-1 に初期化されています。

1.\( p \le k \le i\) (つまり\(p \le k \le p-1\)) を満たすインデックス \(k\) は存在しません。したがって、条件1は自明に（vacuously）真です。
2. \(i+1 \le k \le j-1\) (つまり \(p \le k \le p-1\)) を満たすインデックス \(k\) も存在しません。したがって、条件2も自明に真です。
3. 1行目で x = A[r]と代入されているため、条件3は真です。

よって、ループ開始前にループ不変条件は成り立っています。

維持 (Maintenance):

ループのある反復の開始時点（j の値）で不変条件が真であると仮定し、次の反復の開始時点（j の値が1増えた後）でも真であり続けることを示します。ループ本体では、A[j] とピボット x の比較結果に応じて2つのケースに分岐します。

ケース1: A[j] > x の場合

この場合、ループ内では何も交換されず、i も変化しません。j のみがインクリメントされてループの次の反復に移ります。

1. 領域 A[p...i] は変化していないので、条件1は維持されます。
2. j がインクリメントされると、古い A[j] が A[i+1...j-1] という領域の新しい右端の要素になります。仮定より A[j] > x であったため、この新しい領域のすべての要素が \(x\) より大きいという条件2は維持されます。
3. A[r] は変化しないので条件3も維持されます。

ケース2: A[j] <= x の場合

この場合、5行目で i がインクリメントされ、6行目で A[i] と A[j] が交換されます。
1. i がインクリメントされ、A[j] が新しい A[i] の位置に交換されます。A[j] \(\le\) xであったため、新しい領域 A[p...i] のすべての要素が \(x\) 以下であるという条件1は維持されます。
2. A[i] と交換された元の A[i] は、反復開始時点の不変条件により、\(x\) より大きい値でした（領域 A[i+1...j-1] にあったため）。この値が A[j] の位置に移動します。j がインクリメントされると、この値は新しい領域 A[i+1...j-1] に含まれることになります。したがって、条件2も維持されます。
3. A[r] は変化しないので条件3も維持されます。

以上より、どちらのケースでもループ不変条件は維持されます。

終了 (Termination):

ループは j が p から r-1 まで1ずつ増加するため、r-p 回の反復後に必ず終了します。ループが終了したとき、j=r となっています。この時点でのループ不変条件から何が言えるでしょうか。

1. \(p \le k \le i\) ならば、\(A[k] \le x\)
2. \(i+1 \le k \le r-1\)ならば、\(A[k] > x\)
3. A[r] = x

これは、配列 A[p...r-1] が、A[p...i]（x以下のグループ）と A[i+1...r-1]（x より大きいグループ）に綺麗に分割されたことを意味します。
この後、8行目で A[i+1]と A[r] (ピボット) が交換されます。これにより、ピボットは2つのグループのちょうど中間に配置され、PARTITION の目的が達成されます。最終的なインデックス i+1 を返すことで、呼び出し元の QUICKSORTは次の再帰の範囲を知ることができます。

 PARTITIONの実行時間

PARTITION プロシージャの実行時間は、3-6行目のforループによって支配されます。このループは、部分配列の要素数（ピボットを除く）である\( (r-1) - p + 1 = r-p\)回だけ実行されます。ループ内の処理はすべて定数時間 \(O(1)\) です。したがって、部分配列の要素数を \(n = r-p+1\) とすると、PARTITION の実行時間は \(\Theta(n)\) となります。

クイックソートの性能分析

クイックソートの実行時間は、PARTITION が生成する2つの部分配列のサイズのバランスに大きく依存します。この章では、分割がどのように実行時間に影響を与えるかを、極端なケース（最悪・最良）と、より現実的なケースを通じて直感的に探ります。

 最悪ケース (Worst-Case Partitioning)

クイックソートにとって最悪のシナリオは、PARTITION が常に最も不均衡な分割を生成し続ける場合です。これは、分割後の一方の部分配列が \(n-1\) 個の要素を持ち、もう一方が \(0\) 個の要素を持つ、という状況です。

どのような時、最悪ケースが起こるか？

Lomutoパーティション（最後の要素をピボットにする）では、入力配列が既にソート済みの場合にこの最悪ケースが発生します。例えば [1, 2, 3, 4, 5] で PARTITION を実行すると、ピボット 5 が最大値であるため、他のすべての要素がその「以下」のグループに入り、サイズ4とサイズ0の部分配列が生成されてしまいます。

この状況が再帰の各段階で発生すると、実行時間の漸化式は以下のようになります。

この漸化式を解いてみましょう。

$$
\begin{aligned}
T(n)&=T(n-1)+c n \\
& =(T(n-2)+c(n-1))+c n \\
& =T(n-2)+c((n-1)+n) \\
& =\ldots \\
& =T(1)+c(2+3+\cdots+n) \\
& =c \sum_{k=1}^n k-c=c \frac{n(n+1)}{2}-c=\Theta\left(n^2\right)
\end{aligned}
$$

これは、初項と末項の和に項数をかけて2で割る、算術級数（等差数列の和）の公式です。結果として、最悪実行時間は \(\Theta(n^2)\) となります。これは、ソート済み配列に対して挿入ソートが \(\Theta(n)\) で終わるのと比較すると、非常に残念な結果です。

 最良ケース (Best-Case Partitioning)

一方、クイックソートが最も効率的に動作するのは、PARTITION が常に完全に均等な分割を生成する場合です。つまり、2つの部分配列のサイズがそれぞれ約 \(n/2\) になる状況です。

この場合の漸化式は以下のようになります。

この漸化式は、マージソートの漸化式と全く同じ形をしています。これは、マスター定理（Master Theorem）のケース2に該当し、その解は \(T(n) = \Theta(n \lg n)\) となります。これは、比較ソートアルゴリズムとして知られている理論的な下限に一致する、非常に効率的な実行時間です。

バランスの取れた分割と再帰木

「最悪」と「最良」は両極端な例ですが、現実にはその中間の分割が多く発生します。では、例えば常に9対1のような、一見すると不均衡に見える分割が続いた場合はどうなるでしょうか？

この場合の漸化式は次のようになります。

重要なのは、再帰木の各レベルでのコストの合計が常に \(cn\) となることです。では、この木の深さはどれくらいになるでしょうか？

木は、部分問題のサイズが1になるまで続きます。

• 最も早く葉に到達する経路（毎回 \(1/10\) の方を選ぶ）の深さは、\((1/10)^k n = 1\) を解いて \(k = \log_{10} n\) となります。
• 最も遅く葉に到達する経路（毎回 \(9/10\) の方を選ぶ）の深さは、\((9/10)^k n = 1\) を解いて \(k = \log_{10/9} n\) となります。

対数の底は定数倍の違いしか生まないため、どちらの深さも \(\Theta(\lg n)\) です。つまり、木の深さは \(\Theta(\lg n)\) であり、各レベルのコストは \(\Theta(n)\) です。したがって、総実行時間は、

$$T(n) = (\text{レベル数}) \times (\text{各レベルのコスト}) = \Theta(\lg n) \times \Theta(n) = \Theta(n \lg n)$$

となります。この考察から、分割の比率が（たとえ偏っていても）一定である限り、クイックソートは漸近的に \(\Theta(n \lg n)\) の効率を保つという、非常に強力な特性がわかります。99対1の分割でさえ、実行時間は \(\Theta(n \lg n)\) です。問題なのは、分割比が \(n-1\) 対 \(0\) のように、定数ではなく \(n\) に依存する形で偏る場合なのです。

平均ケースに関する直観

実際のランダムな入力データに対しては、ある時は均等に近い「良い」分割が、またある時は偏った「悪い」分割が、ランダムに混ざり合って発生すると考えられます。

ここで面白いのは、「悪い」分割の影響が、「良い」分割によってうまく相殺されるという点です。
次のシナリオを考えてみましょう。

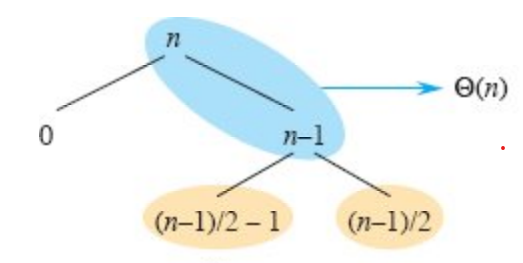
1. レベル0: 根でサイズ \(n\) の問題に対し、「悪い」分割が発生。コストは \(\Theta(n)\)で、サイズ \(n-1\) と \(0\) の部分問題が生成される。
2. レベル1: サイズ \(n-1\) の問題に対し、「良い」分割が発生。コストは \(\Theta(n-1)\) で、サイズ約 \((n-1)/2\) の部分問題が2つ生成される。

この2レベルをまとめて考えてみると、合計コストは \(\Theta(n) + \Theta(n-1) = \Theta(n)\) であり、結果として3つの部分問題（サイズ0, 約\(n/2\), 約\(n/2\)）が残ります。これは、最初から1回の「良い」分割で2つのサイズ約\(n/2\)の部分問題が生成されるのと、大差ありません。

直感的には、「悪い」分割で発生したコスト \(\Theta(n-1)\) が、直後の「良い」分割のコスト \(\Theta(n)\) に吸収されてしまい、全体としてはバランスの良い分割が行われたかのように振る舞うのです。この幸運な組み合わせのおかげで、クイックソートの平均的な性能は最良ケースに非常に近くなる、と期待できます。

 ランダム化による性能改善

ここまでは、「入力データがランダムである」という仮定のもとでの「平均的な」振る舞いでした。しかし、現実世界のデータが常にランダムであるとは限りません。例えば、ほとんどソート済みのデータを扱う場面は頻繁にあります。このような特定の入力パターンに対して、決定的なアルゴリズム（例えば、常に最後の要素をピボットに選ぶクイックソート）は、常に最悪の \(\Theta(n^2)\) の性能を示してしまいます。

この問題を解決し、いかなる入力に対しても良好な平均性能を保証するための強力な手法がランダム化 (Randomization) です。

なぜランダム化が必要か？

決定性アルゴリズムの弱点は、その動作が入力に完全に依存しているため、アルゴリズムの弱点を突くような「キラー入力」が存在し得ることです。悪意のあるユーザーがそのような入力を与えれば、システムをサービス不能攻撃（DoS）に陥れることさえ可能です。

ランダム化は、アルゴリズムの動作に偶然性を持ち込むことで、この問題を回避します。アルゴリズムの振る舞いが入力だけでなく、アルゴリズム内で生成される乱数にも依存するようになるため、特定の入力が常に最悪のパフォーマンスを引き起こす、ということがなくなります。運が悪ければ遅くなる可能性は残りますが、その「運の悪さ」は入力データとは無関係になります。これにより、性能は入力の構造ではなく、確率に支配されるようになり、期待実行時間という形で性能を保証できるようになります。

ランダム化クイックソートのアイデア

クイックソートをランダム化する最も簡単で効果的な方法は、ピボットの選択をランダムに行うことです。

• 決定性クイックソート: 常に部分配列 A[p...r] の最後の要素 A[r] をピボットにする。
• ランダム化クイックソート: 部分配列 A[p...r] の中から、一様ランダムに一つの要素を選び、それをピボットとする。

これにより、入力配列がどのような順序であっても、ピボットが極端に大きい値や小さい値になる可能性は低くなり、分割がほどよくバランスされることが期待できます。

RANDOMIZED-QUICKSORT プロシージャ

このアイデアを実装するのは驚くほど簡単です。既存の PARTITION プロシージャをそのまま利用し、その前処理としてランダムなピボット選択を追加するだけです。

pseudocode
RANDOMIZED-PARTITION(A, p, r)
1  // pからrまでの範囲でランダムなインデックスiを選ぶ
2  i = RANDOM(p, r)
3  // 選んだ要素A[i]を、PARTITIONがピボットとして使う最後の要素A[r]と交換する
4  exchange A[r] with A[i]
5  // 元のPARTITIONを呼び出す
6  return PARTITION(A, p, r)

RANDOMIZED-QUICKSORT(A, p, r)
1  if p < r
2      // PARTITIONの代わりにRANDOMIZED-PARTITIONを呼び出す
3      q = RANDOMIZED-PARTITION(A, p, r)
4      RANDOMIZED-QUICKSORT(A, p, q - 1)
5      RANDOMIZED-QUICKSORT(A, q + 1, r)

変更点は、QUICKSORT が PARTITION の代わりに RANDOMIZED-PARTITION を呼び出すようになったことだけです。そして RANDOMIZED-PARTITION は、ランダムに選んだ要素を A[r] と交換するという、たった2行の前処理を追加しただけです。このわずかな変更が、クイックソートを特定の入力に弱い脆弱なアルゴリズムから、いかなる入力にも頑健な高性能アルゴリズムへと変貌させるのです。

厳密な性能分析

この章では、これまで直感的に議論してきたクイックソートの性能を、数学的に厳密に分析します。まず最悪ケースの実行時間が \(\Theta(n^2)\) であることを証明し、次に本題であるランダム化クイックソートの期待実行時間が \(\Theta(n \lg n)\) となることを導出します。

 最悪ケース分析 (Worst-Case Analysis)

ランダム化を行ったとしても、確率的な事象である以上、常に最悪のピボットが選ばれ続けるという「極めて不運な」シナリオは理論上存在します。したがって、RANDOMIZED-QUICKSORT の最悪実行時間は、決定性バージョンと変わらず \(\Theta(n^2)\) です。ここでは、その上界が \(O(n^2)\) であることを代入法 (Substitution Method) を用いて証明します。
クイックソートの最悪実行時間 \(T(n)\) は、サイズ \(q\) と \(n-1-q\) の分割（\(0 \le q \le n-1\)）のうち、最も実行時間が長くなるものによって決まるため、以下の漸化式で表せます。

$$T(n) = \max_{0 \le q \le n-1} \{T(q) + T(n-1-q)\} + \Theta(n)$$

証明:
私たちは、\(T(n) \le cn^2\) がある定数 \(c > 0\) に対して成り立つと推測し、これを数学的帰納法で証明します。

\(T(n) \le \max_{0 \le q \le n-1} \{cq^2 + c(n-1-q)^2\} + \Theta(n)\)
\(= c \cdot \max_{0 \le q \le n-1} \{q^2 + (n-1-q)^2\} + \Theta(n)\)

ここで、関数 \(f(q) = q^2 + (n-1-q)^2\) の最大値を考えます。これは \(q\) に関する二次関数で、グラフは下に凸の放物線を描きます。したがって、最大値は定義域の端点、つまり \(q=0\) または \(q=n-1\) で取られます。
\(q=0\) のとき、\(f(0) = 0^2 + (n-1)^2 = (n-1)^2\)
\(q=n-1\) のとき、\(f(n-1) = (n-1)^2 + 0^2 = (n-1)^2\)
よって、\(\max_{0 \le q \le n-1} \{q^2 + (n-1-q)^2\} = (n-1)^2\) です。

これを元の不等式に戻します。

\(T(n) \le c(n-1)^2 + \Theta(n)\)
\(= c(n^2 - 2n + 1) + \Theta(n)\)
\(= cn^2 - 2cn + c + \Theta(n)\)

この式が \(cn^2\) 以下であることを示すには、\(-2cn + c + \Theta(n) \le 0\) が成り立てばよいです。\(\Theta(n)\) は、ある定数 \(d > 0\) を用いて \(dn\) と書けるので、

\(-2cn + c + dn \le 0\)
\(c - (2c - d)n \le 0\)

この不等式が十分に大きな \(n\) で成り立つためには、係数 \((2c-d)\) が正であれば十分です。つまり、\(c > d/2\) となるように定数 \(c\) を十分に大きく選べば、この条件は満たされます。

したがって、\(T(n) = O(n^2)\) が証明されました。2.1節で示したように、ソート済み配列が \(\Omega(n^2)\) の実行時間を引き起こすため、合わせて最悪実行時間は \(\Theta(n^2)\) と結論付けられます。

期待実行時間分析 (Expected Running Time Analysis)

ここからが本題です。RANDOMIZED-QUICKSORT の期待実行時間を分析します。分析を簡単にするために、いくつかのステップを踏みます。（※ここからの分析では、簡単のため配列の要素はすべて異なると仮定します。）

準備1: 実行時間と総比較回数 (補題 1)

まず、アルゴリズムの実行時間を、より数えやすい指標である要素間の比較回数に関連付けます。

証明:
QUICKSORT の実行時間は、PARTITION プロシージャで費やされる時間によって支配されます。

• PARTITION の呼び出し回数: 各呼び出しで選択されたピボットは、その後の再帰では二度と考慮されません。要素は \(n\) 個しかないので、PARTITION の呼び出しは高々 \(n\) 回です。
• PARTITION 内のコスト: PARTITION のコストは、for ループのコストとその外の定数時間のコストからなります。

* ループ外のコスト: 1回の呼び出しで \(O(1)\) なので、合計でも \(O(n)\) です。
* ループ内のコスト: for ループの各反復で、4行目の if A[j] <= x で1回の比較が行われます。したがって、アルゴリズム全体での for ループの総実行時間は、総比較回数 \(X\) に比例し、\(\Theta(X)\) となります。
以上を合計すると、総実行時間は \(O(n) + \Theta(X) = O(n+X)\) となります。

この補題により、私たちの目標は、確率変数 \(X\) の期待値 \(E[X]\) を求めることに絞られました。\(E[X]\) が \(O(n \lg n)\) であることを示せれば、期待実行時間も \(O(n \lg n)\) となります。

準備2: どの要素ペアが比較されるか？ (補題 2)

次に、どの2つの要素が比較され、どのペアが比較されないのかを正確に特徴づけます。分析を容易にするため、入力配列の要素を、ソート後の順序で名前を付け直します。すなわち、\(z_1, z_2, \dots, z_n\) とし、ここで \(z_1 < z_2 < \dots < z_n\) です。また、集合 \(\{z_i, z_{i+1}, \dots, z_j\}\) を \(Z_{ij}\) と表記します。

証明:
集合 \(Z_{ij}\) に属する要素が、アルゴリズムの実行中に初めてピボットとして選ばれる瞬間を考えます。

• ケース1: \(z_k\) (\(i < k < j\)) が最初にピボットとして選ばれた場合。

このとき、PARTITION は配列を \(z_k\) の周りで分割します。\(z_i < z_k < z_j\) なので、\(z_i\) は \(z_k\) 以下のグループに、\(z_j\) は \(z_k\) 以上のグループに分けられます。これ以降、\(z_i\) と \(z_j\) が同じ部分配列に含まれることは決してないため、この2つが比較されることはありません。

• ケース2: \(z_i\) が最初にピボットとして選ばれた場合。

\(z_i\) がピボットになると、PARTITION は \(z_i\) を部分配列内の他のすべての要素と比較します。この部分配列には \(z_j\) も含まれているため、\(z_i\) と \(z_j\) は比較されます。

• ケース3: \(z_j\) が最初にピボットとして選ばれた場合。

ケース2と同様に、\(z_j\) がピボットとなり、\(z_i\) と比較されます。

したがって、補題は証明されました。この洞察は、確率計算の鍵となります。

 準備3: 2要素が比較される確率 (補題 3)

補題7.2を基に、\(z_i\) と \(z_j\) が比較される確率を計算します。

証明:
補題7.2より、この確率は「集合 \(Z_{ij}\) の中で、\(z_i\) または \(z_j\) が最初にピボットとして選ばれる確率」と等価です。
RANDOMIZED-PARTITION はピボットを一様ランダムに選択します。\(z_i\) と \(z_j\) がまだ同じ部分配列にある限り、集合 \(Z_{ij}\) の \(|Z_{ij}| = j-i+1\) 個の要素は、その中から最初にピボットとして選ばれる確率はすべて等しくなります。
したがって、

• \(Z_{ij}\) の中で \(z_i\) が最初に選ばれる確率は \(1/(j-i+1)\)
• \(Z_{ij}\) の中で \(z_j\) が最初に選ばれる確率は \(1/(j-i+1)\)

この2つの事象は互いに排反（同時に起こらない）なので、求める確率はこれらの和となります。

\(\text{Pr}\{z_i \text{ is compared with } z_j\} = \frac{1}{j-i+1} + \frac{1}{j-i+1} = \frac{2}{j-i+1}\)

主証明: 期待実行時間の導出 (定理 4)

いよいよ、これまでの準備を統合して、期待比較回数 \(E[X]\) を計算します。

証明:
総比較回数 \(X\) は、すべての要素ペア \((z_i, z_j)\) (\(i<j\)) について、それらが比較されるかどうかで決まります。ここで指示確率変数 (Indicator Random Variable) \(X_{ij}\) を導入します。

\(X_{ij} = I\{z_i \text{ と } z_j \text{ が比較される}\} = \begin{cases} 1 & \text{if } z_i \text{ and } z_j \text{ are compared} \\ 0 & \text{otherwise} \end{cases}\)

すると、総比較回数 \(X\) はこれらの和として表現できます。

\(X = \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} X_{ij}\)

期待値の線形性により、和の期待値は期待値の和と等しくなります。

\(E[X] = E \left[ \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} X_{ij} \right] = \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} E[X_{ij}]\)

指示確率変数の期待値は、それが1となる確率に等しいので、\(E[X_{ij}] = \text{Pr}\{z_i \text{ と } z_j \text{ が比較される}\}\) です。補題7.3の結果を代入します。

\(E[X] = \sum_{i=1}^{n-1} \sum_{j=i+1}^{n} \frac{2}{j-i+1}\)

この二重和を評価します。内側の和のインデックスが複雑なので、変数変換 \(k=j-i\) を行います。\(i\) を固定したとき、\(j\) が \(i+1\) から \(n\) まで動くと、\(k\) は \(1\) から \(n-i\) まで動きます。

\(E[X] = \sum_{i=1}^{n-1} \sum_{k=1}^{n-i} \frac{2}{k+1}\)

ここで、内側の和 \(\sum_{k=1}^{n-i} \frac{2}{k+1}\) を評価します。これは調和級数の一部に似ています。
\(\sum_{k=1}^{n-i} \frac{2}{k+1} < \sum_{k=1}^{n-1} \frac{2}{k+1} < \sum_{m=2}^{n} \frac{2}{m}\) (ここで \(m=k+1\))
調和級数 \(H_n = \sum_{k=1}^{n} \frac{1}{k}\) は \(\ln n + O(1)\) と近似できるので、この和は \(O(\lg n)\) です。

\(E[X] < \sum_{i=1}^{n-1} O(\lg n)\)

外側の和は \(n-1\) 個の項を持つので、

\(E[X] = (n-1) \cdot O(\lg n) = O(n \lg n)\)

総期待比較回数 \(E[X]\) が \(O(n \lg n)\) であることが示されました。補題7.1より、期待実行時間は \(O(n + E[X]) = O(n + n \lg n) = O(n \lg n)\) となります。最良ケースが \(\Omega(n \lg n)\) であることから、期待実行時間は \(\Theta(n \lg n)\) であると結論付けられます。

さらなる考察と発展的トピック

クイックソートは非常に奥が深いアルゴリズムであり、実用的な実装には様々な改良が施されています。ここでは、教科書で演習問題として扱われるいくつかの重要なトピックを解説します。

 等しい要素への対処 (3-way Partitioning)

これまでの分析では、配列の要素がすべて異なると仮定していました。しかし、要素に重複が多い場合、Lomuto法では性能が劣化する可能性があります。例えば、すべての要素が同じ値の配列では、最悪ケースの \(\Theta(n^2)\) となってしまいます。

この問題に対処する効果的な方法が 3-way Partitioning です。この手法では、配列を以下の3つの領域に分割します。

1. ピボットより小さい要素
2. ピボットと等しい要素
3. ピボットより大きい要素

分割後は、中央の「等しい」要素のグループはソート済みと見なせるため、再帰呼び出しは左右の「小さい」「大きい」グループに対してのみ行います。これにより、重複が多いデータに対する効率が劇的に向上します。

ピボット選択の改良 (3要素の中央値)

ランダム化は理論的に優れた性能を保証しますが、高品質な乱数を生成するにはコストがかかります。実用上、性能を安定させるためのヒューリスティクスとして3要素の中央値 (Median-of-three) と呼ばれる手法がよく用いられます。
これは、部分配列の先頭、中央、末尾の3つの要素を取り出し、その中央値をピボットとして選択する手法です。これにより、ピボットが極端な値になる確率を大幅に減らし、よりバランスの取れた分割を安定して生成することが期待できます。

まとめと参考文献

本記事では、クイックソートの基本アルゴリズムから、その性能を支える理論的背景、そして実用的な改良に至るまでを包括的に解説しました。

• クイックソートは分割統治法に基づくアルゴリズムで、その核心はPARTITION`プロシージャにある。
• 性能は分割のバランスに依存し、最悪 \(\Theta(n^2)\)、最良 \(\Theta(n \lg n)\) となる。
• ランダム化によりピボットを選択することで、いかなる入力に対しても \(\Theta(n \lg n)\) の期待実行時間を達成できる。
• その厳密な証明には、指示確率変数と期待値の線形性が強力なツールとなる。
• 実用的な実装では、Hoareの分割法、3-way Partitioning、スタック深度の最適化など、様々な改良が加えられている。

クイックソートは、1959年にC. A. R. Hoareによって発明されて以来、その卓越した平均性能と効率性から、アルゴリズムの世界で不動の地位を築いてきました。その分析を通じて、私たちはアルゴリズム設計における理論と実践の美しい結びつきを垣間見ることができます。